6 Introdução à Análise Estatística Espacial
6.1 O que é Análise Estatística Espacial?
São métodos estatísticos que levam em consideração a localização espacial do fenômeno estudado;
Define-se “Análise estatística espacial quando os dados são espacialmente localizados e se considera explicitamente a possível importância de seu arranjo espacial na análise ou interpretação dos resultados” (Bailey & Gatrell, 1995).
Principal característica: a localização geográfica é utilizada explicitamente na análise.
Neste curso serão abordadas basicamente as técnicas estatísticas de análise espacial.
Diversas operações realizadas em um SIG são também chamadas de análise espacial, mas não são objeto deste curso.
6.2 Origem da Estatística Espacial
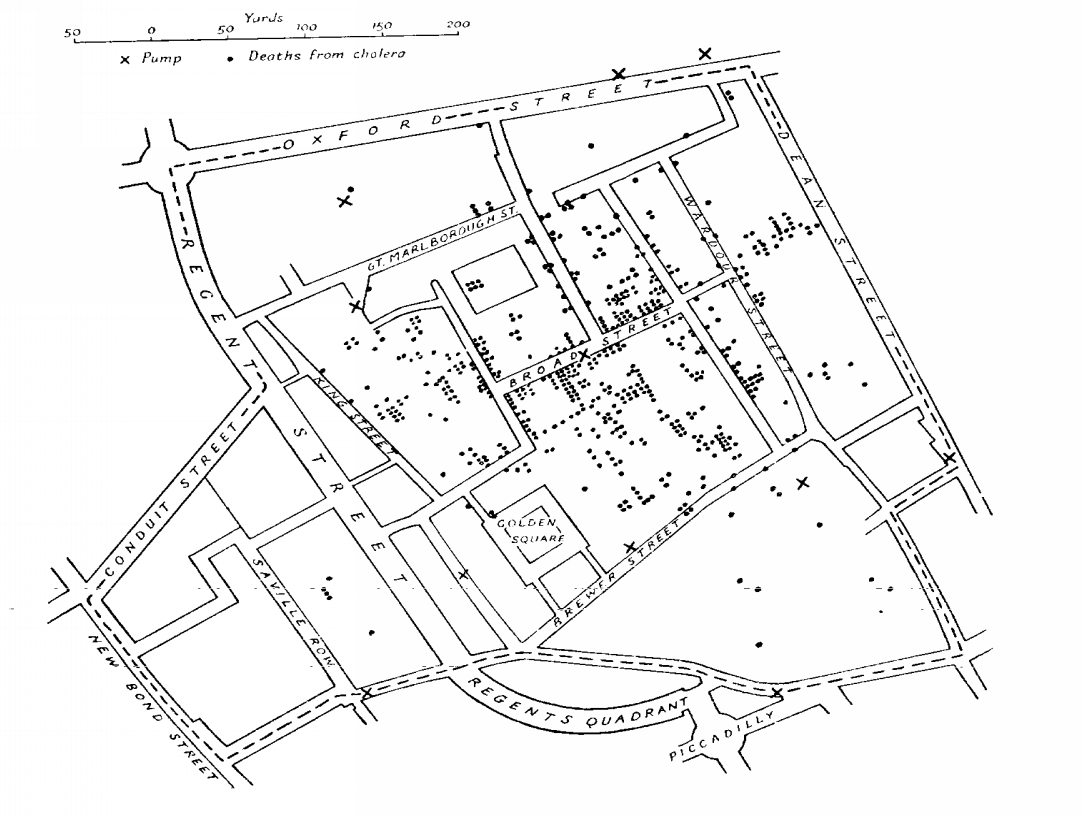
- Dr. John Snow (1813-1858) Considerado pai da Epidemiologia Moderna:

- Mapeamento dos casos de coléra (\(\bullet\)) e as bombas de água (X). (Londres, 1854)
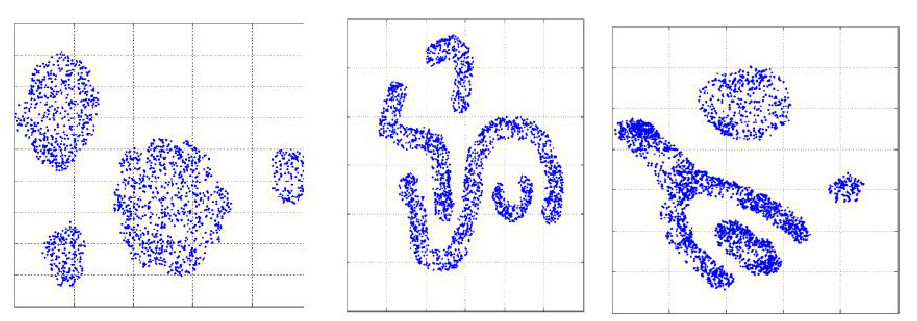
6.3 Quando usar métodos de análise espacial?
- A primeira pergunta a ser feita é: A distribuição dos dados apresenta um padrão aleatório ou apresenta algum outro tipo de padrão? (Tendências, clusters, Regular)
Heterogeneidade espacial: A magnitude e a direção do fenômeno de interesse varia no espaço.
Violação da suposição de independência: Os atributos da observação i influenciam nos atributos na observação j.
6.4 Dependência espacial
- A visão da Geografia
Conhecida como 1\(^a\) Lei da Geografia!
“Todas as coisas são parecidas, mas coisas mais próximas se parecem mais que coisas mais distantes.”
(Waldo Tobler, 1979) wikipedia
- Quais as possíveis implicações de não considerar a localização espacial na modelagem?
Dependência Estatística Espacial
“Independência é um pressuposto muito conveniente que faz grande parte da teoria estatı́stica matemática tratável. Entretanto, modelos que envolvem dependência estatı́stica são freqüentemente mais realı́sticos. […] dados espaciais, onde a dependência está presente em todas as direções e fica mais fraca a medida em que aumenta a dispersão na localização dos dados.” (Noel Cressie, Statistics for spatial data. 1991)
Generalizando, a maior parte dos fenômenos, sejam estes socioeconômicos ou da área da saúde, apresentam entre si uma relação - semelhança ou inibição - que depende da distância.
6.5 Principais aplicações em Saúde
Mapeamento de doenças: O objetivo geral é avaliar a variação geográfica na ocorrência das doenças visando identificar diferenciais de risco, orientar a alocação de recursos, levantar hipóteses etiológicas.
Clusters: O objetivo da detecção de cluster espacial é estabelecer a significância de um sobrerrisco em um determinado espaço ou tempo e espaço. Este cluster pode ser causado por diferentes fatores: agentes infecciosos, contaminação ambiental localizada, efeitos colaterais de tratamentos, etc.
Estudos ecológicos: Essencialmente modelos de regressão, onde se busca explicar a variação na incidência da doença através de outras variáveis.
Avaliação e monitoramento ambiental: Estimativa e monitoramento da distribuição espacial de fatores ambientais relevantes para a saúde. Por exemplo, poluentes químicos, insolação (Raios UV), vegetação, clima, etc.
A quantidade e disponibilidade de dados nesta área atualmente é bem grande, com ênfase particular para as imagens de satélite, com resolução e acessibilidade cada vez maiores.
6.6 Tipologia dos dados espaciais
Os diferentes tipos de dados espaciais são tradicionalmente classificados de acordo com uma tipologia. Esta caracterização diz respeito a natureza estocástica da observação.
Cressie divide a estatística espacial em 3 grandes áreas:
Dados de processos pontuais;
Dados de geoestatística;
Dados de área;
Existem métodos estatísticos diferentes para descrever ou analisar estes tipos de dados.
| Tipo de Dado | Exemplos | Técnicas | |
|---|---|---|---|
| Análises de padrões pontuais | Eventos localizados | Ocorrência de doenças | - Determinação de Padrões - Cluster |
| Geoestatística | Amostras | Variáveis ambientais | - Interpolação de superfícies |
| Análises de dados de Área | Atributos de um polígono | Dados censitários | - Correlação espacial * modelos de Regressão |
OBSERVAÇÃO!
Existem ainda outros tipos de dados como por exemplo imagens de satélites (RASTER), redes e fluxos que não serão vistos nesse curso.
Eventualmente misturas de diferentes tipos de dados estão presentes em um mesmo estudo.
Em algumas situações pode-se converter o dado de um tipo para outro (troca de suporte).
6.7 Dados de Processos Pontuais
O principal interesse está no conjunto de coordenadas geográficas representando as localizações exatas de eventos.
Exemplos: Localização de crimes, localização da residência dos casos de dengue, localização de espécies vegetais, etc.
Neste caso, o dado aleatório de interesse é a localização espacial do evento.
O objetivo é estudar a distribuição espacial dos pontos testando a hipótese sobre o padrão observado: existe aglomeração/cluster de casos ou eles estão dispostos aleatoriamente?
- Localização da ocorrência de todos os crimes violentos no ano de 1998 registrados pela PM de Belo Horizonte:
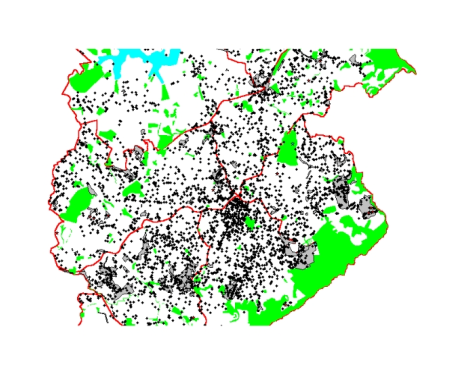
Existe aglomeração de casos em alguma área da cidade?
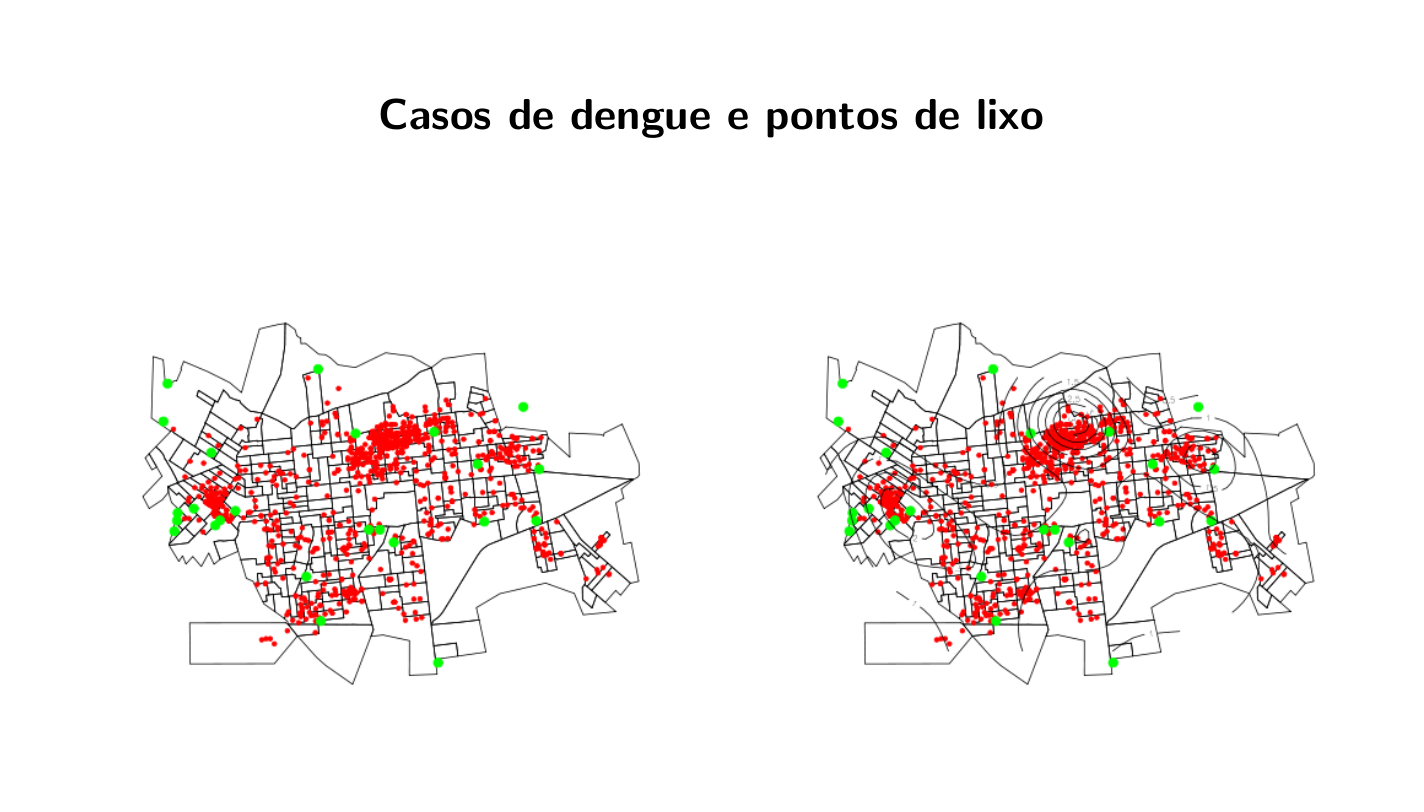
- Localização da ocorrência de casos de Dengue em Belo Horizonte: (Jean Barrado)
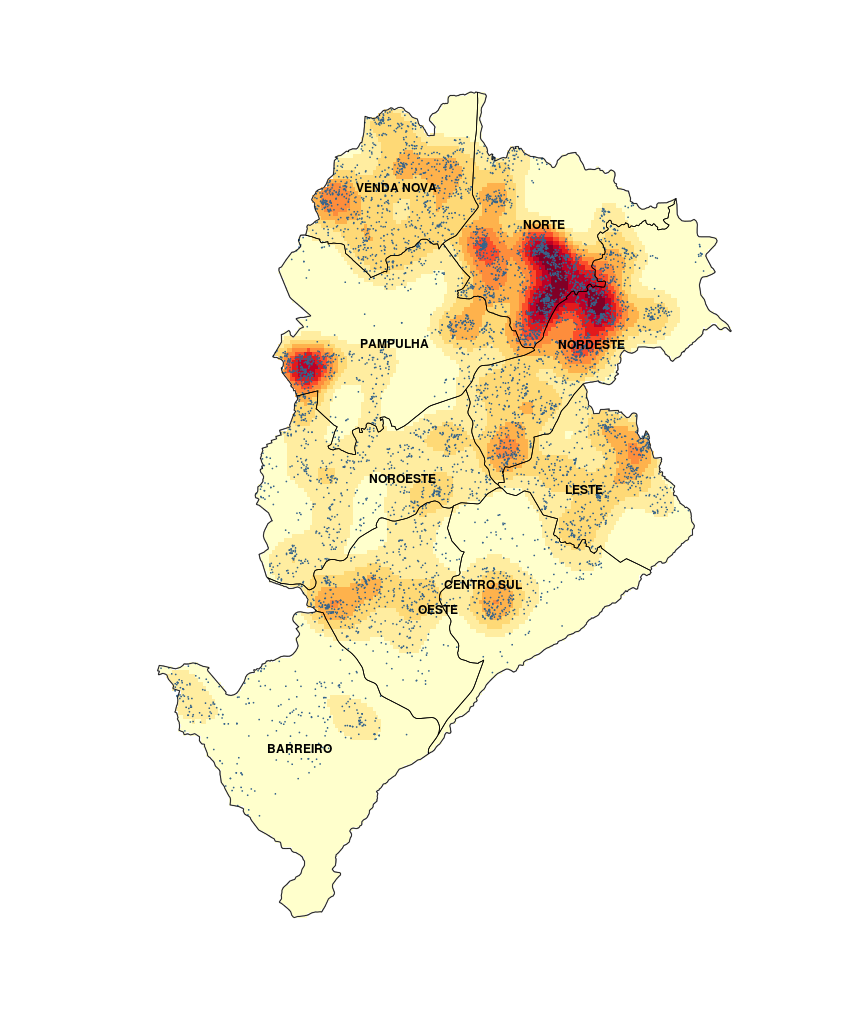
- Detection and modelling of case clusters for urban leptospirosis:
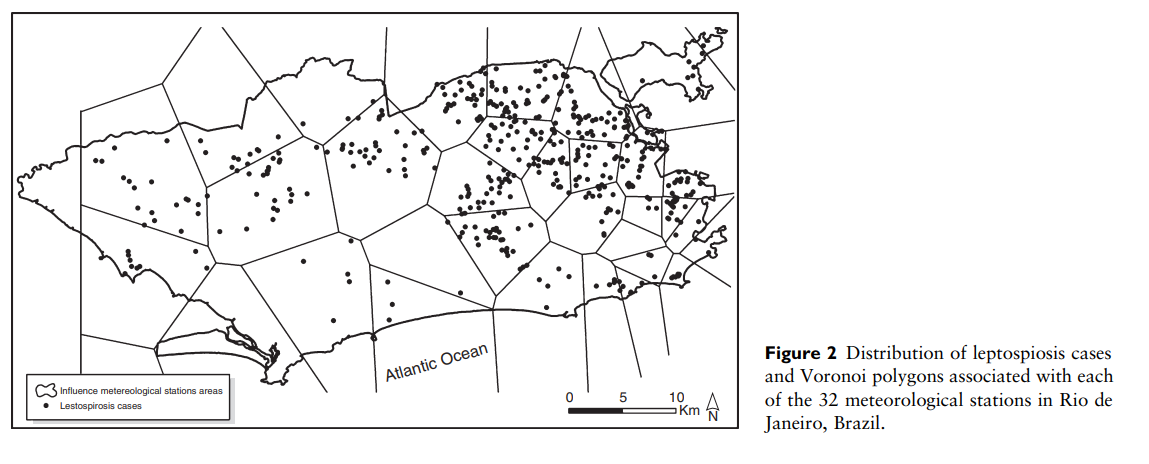
Fonte: Tassinari et al. (2008).
- Spatial distribution of leptospirosis in the city of Rio de Janeiro, Brazil, 1996-1999:
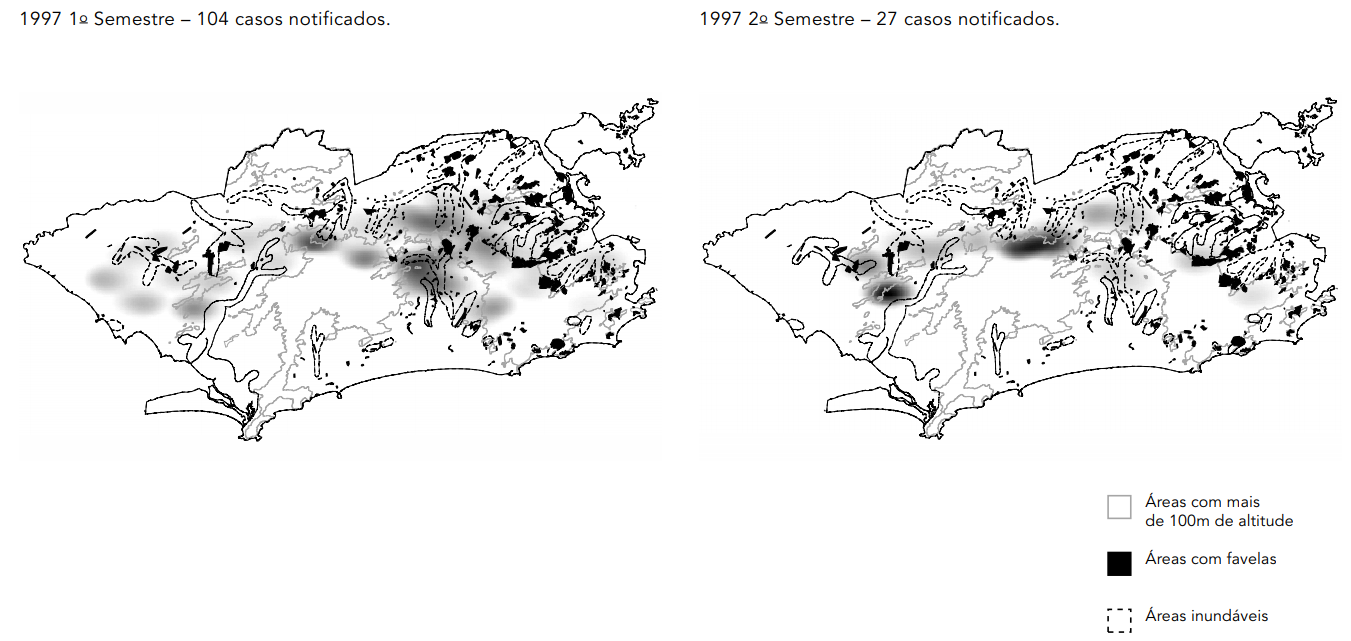
6.8 Geoestatı́stica
São dados que compreendem um conjunto de localizações (em geral latitudes e longitudes), mas agregados a eles uma medida contínua, como por exemplo o volume de chuva.
Neste caso estaremos interessados em entender o padrão nos valores amostrados nestas localizações e também modelar e estimar valores em localizações não medidas.
Bastante utilizada em ciências ambientais (chuva, temperatura, umidade, poluentes no ar, etc.)
Exemplo: Mapa sobre o teor de argila no solo.
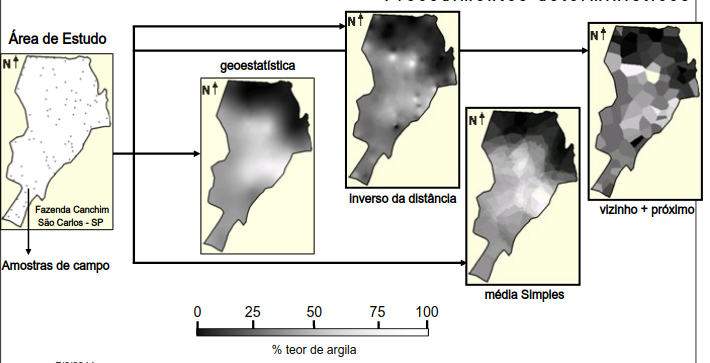
- Krigagem da chuva no Rio de Janeiro
6.9 Dados de Área
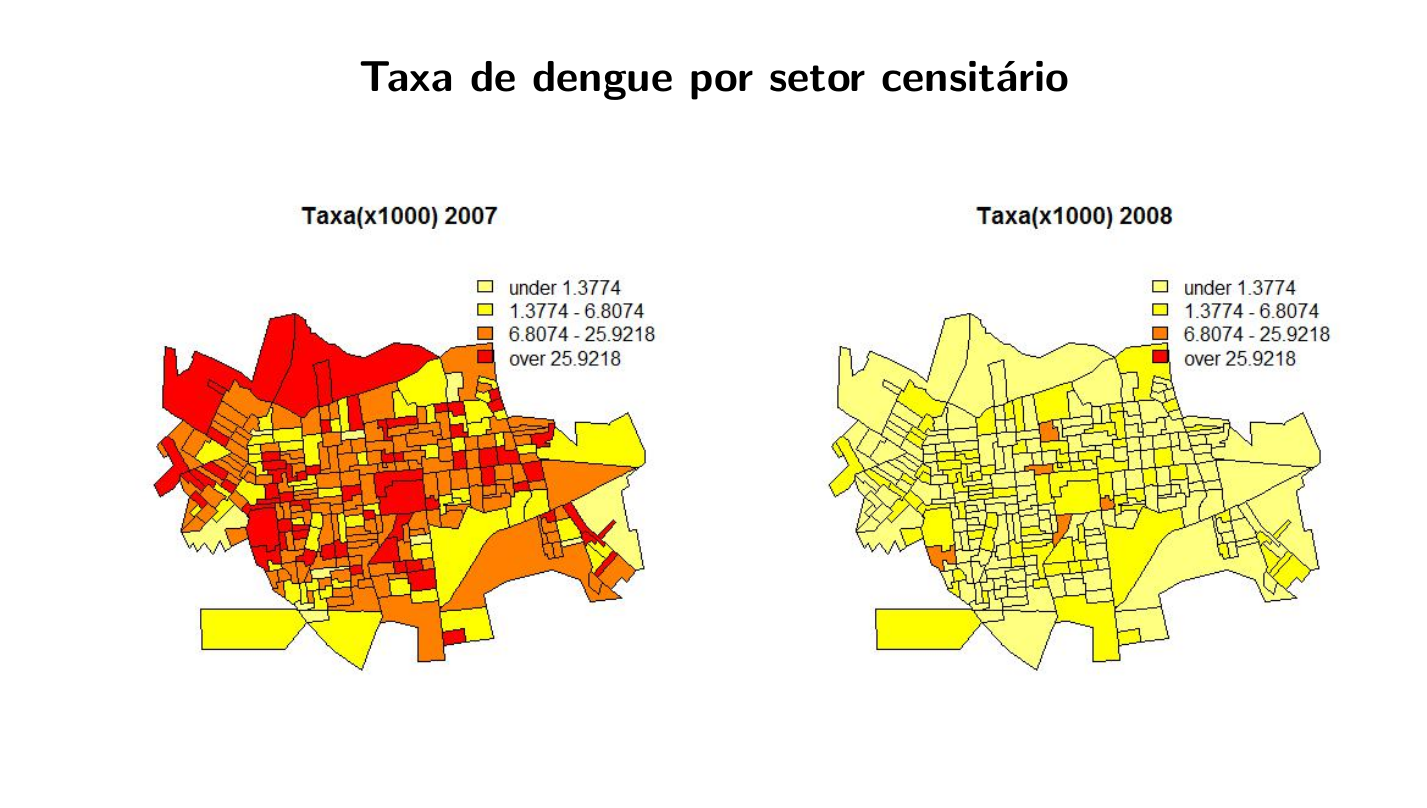
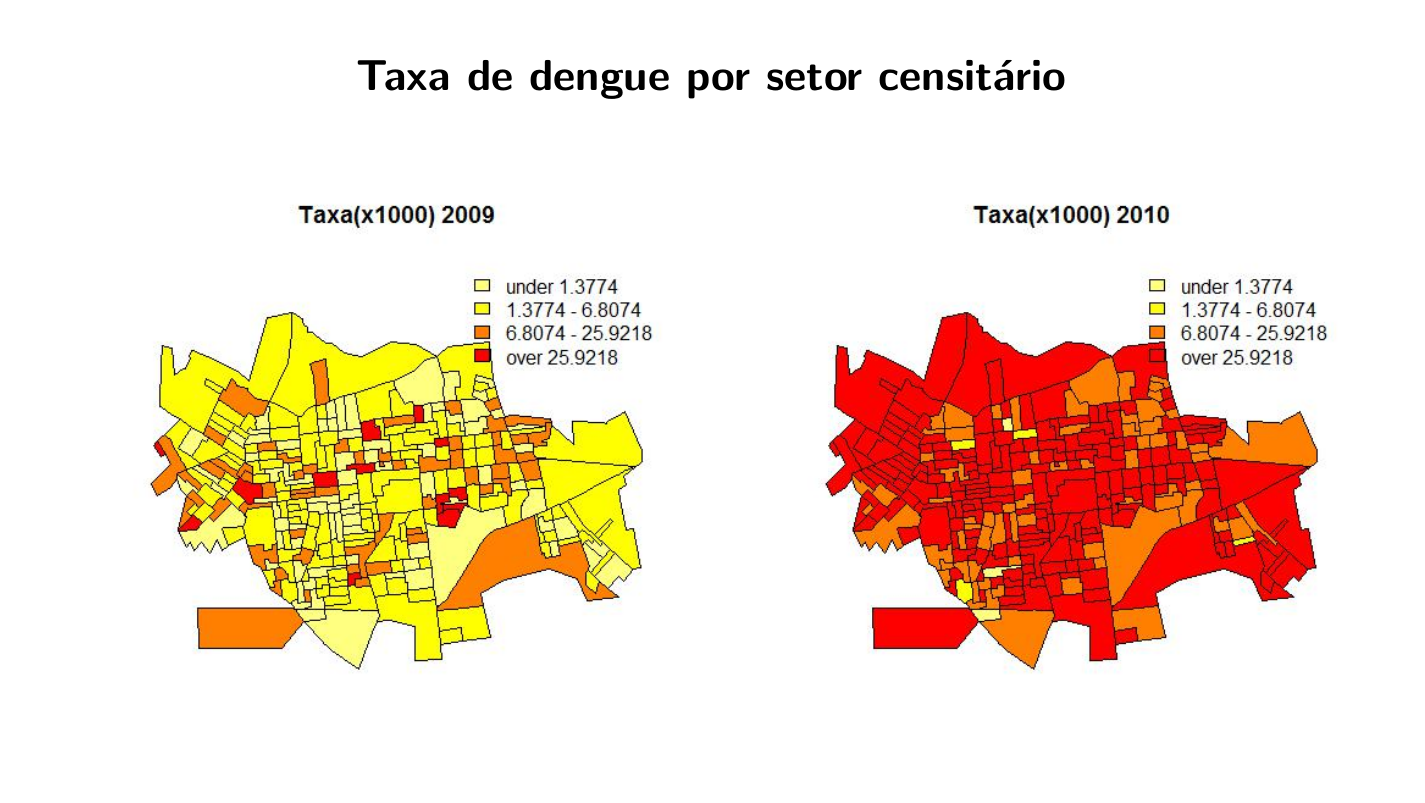
Este tipo de dado pode ser visualizado em mapas onde o espaço é particionado em áreas e cada área é colorida de acordo com alguma variável.
As áreas podem ser:
- Irregulares: divisões de caráter polı́tico ou administrativo. Por exemplo: municípios, setores censitários, etc.
- Regulares: medidas em grade regular. Por exemplo, imagens de satélite.
Para cada uma destas áreas temos informações agregadas de um determinado fenômeno (em geral somas ou médias).
Bastante utilizados em epidemiologia, economia e demografia, etc.
Objetivo: Identificar áreas de risco.
-Taxas de câncer de pulmão na população branca masculina nos Estados Unidos, por condados no ano de 1998:
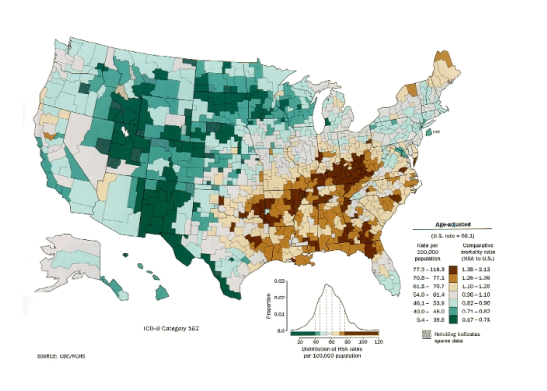
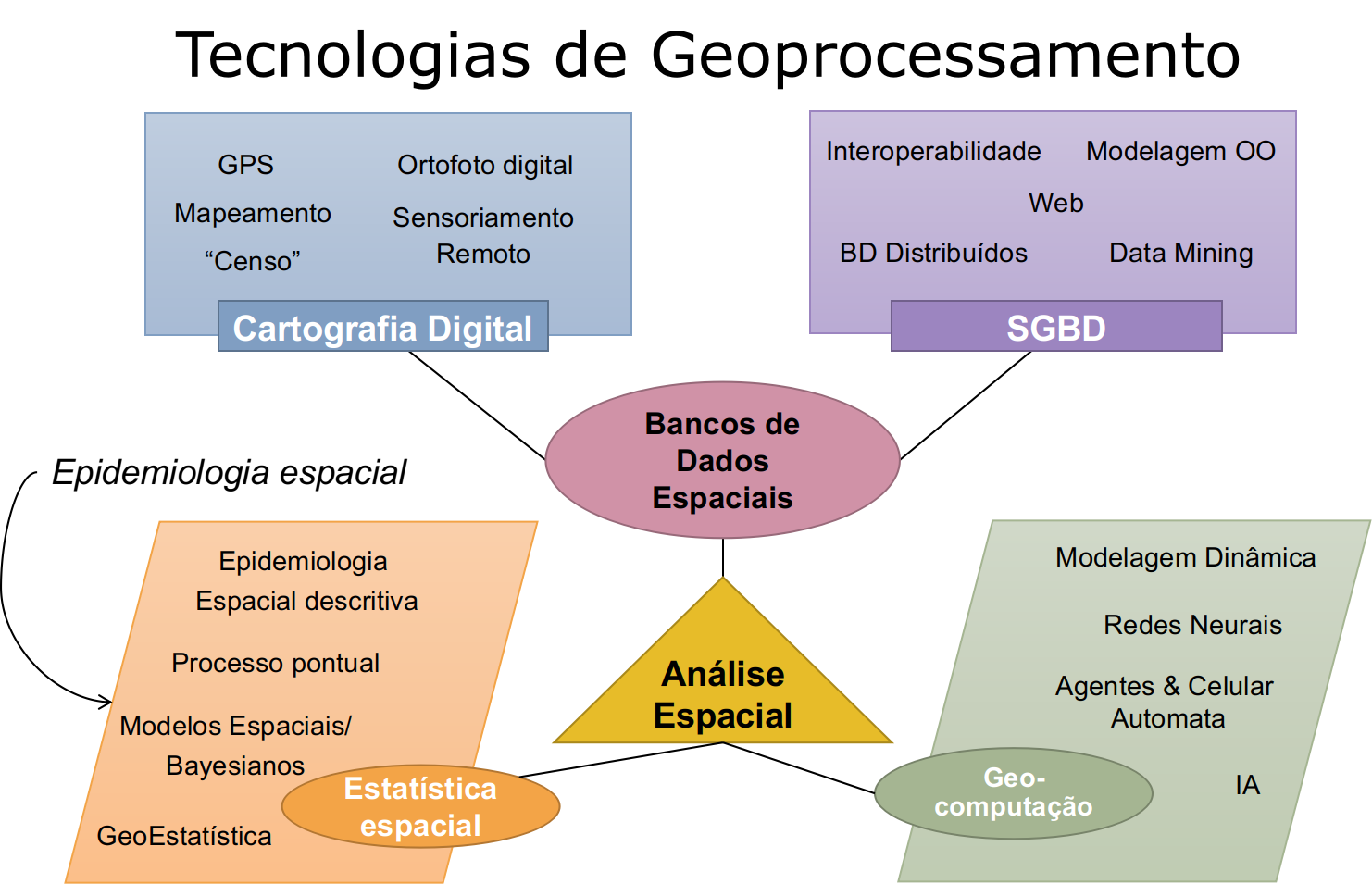
6.10 Geoprocessamento
Geoprocessamento é um conjunto de técnicas , softwares e hardware capazes de coletar , tratar , analisar e disseminar informações georreferenciadas permitindo o desenvolvimento de novos dados, analises e aplicações;
Utiliza programas de computador que permitem o uso integrado de informações cartográficas (mapas, cartas topográficas , imagens de satélites etc…) e informações tabulares (dados alfanumericos) e possibilita se associar coordenadas desses dados a mapas ;
Duas das principais ferramentas de geoprocessamento são os Sistema de Informações Geográficas (SIG) e o Sensoriamento Remoto (SR)
Este curso não vai abordar a tecnologias de Sensoriamento Remoto ainda que exista a possibilidade, cada vez maior de se integrar todas as técnicas usando o R.
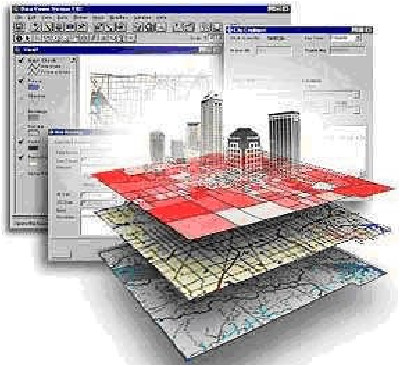
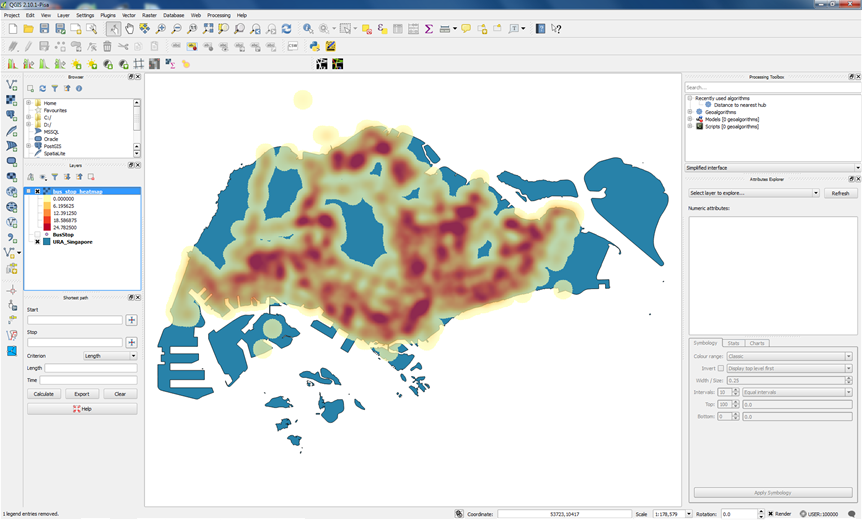
6.12 Sistema de Informações Geográficas
Um Sistema de Informação Geográfica (SIG ou GIS - Geographic Information System) é um sistema de hardware, software, informação espacial e procedimentos computacionais que permite e facilita a análise, gestão ou representação do espaço e dos fenômenos que nele ocorrem.
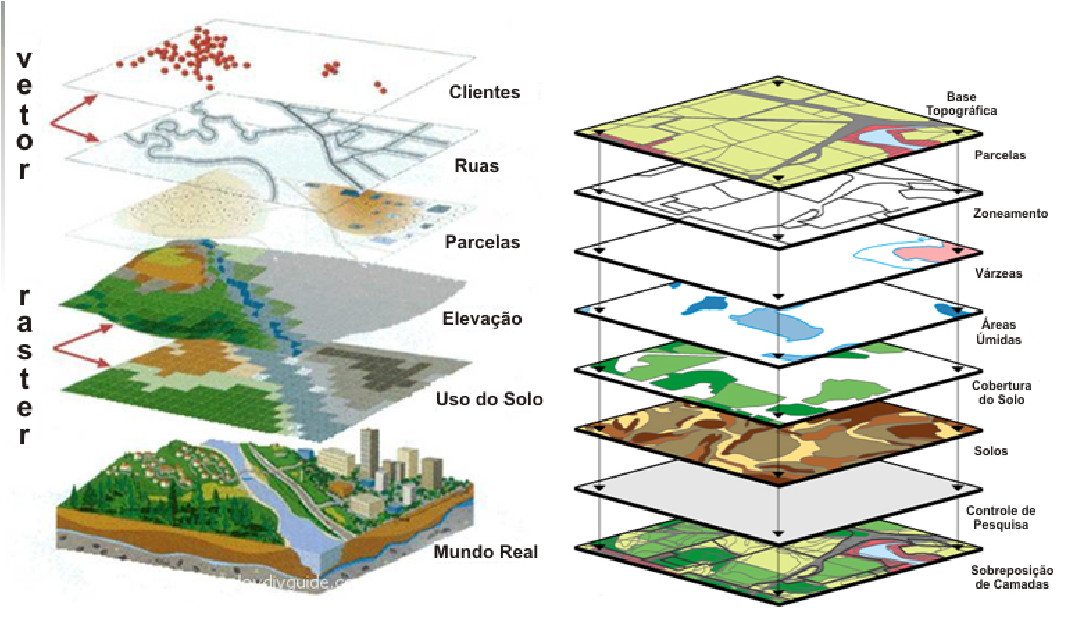
6.14 Alguns Conceitos
6.14.1 Autocorrelação espacial
É uma medida estatística que quantifica e testa o grau de dependência entre observações no espaço.
Caso haja evidência de estrutura espacial, o postulado de independência das amostras, é inválido.
Nestes casos os modelos de regressão devem levar em conta explicitamente o espaço em suas formulações.
Dados espaciais são considerados uma única realização de um processo estocástico. Diferente da amostragem tradicional, em que cada observação traz uma informação independente, todas as observações são utilizadas de forma conjunta para descrever o padrão do fenômeno estudado.
6.15 Aplicações
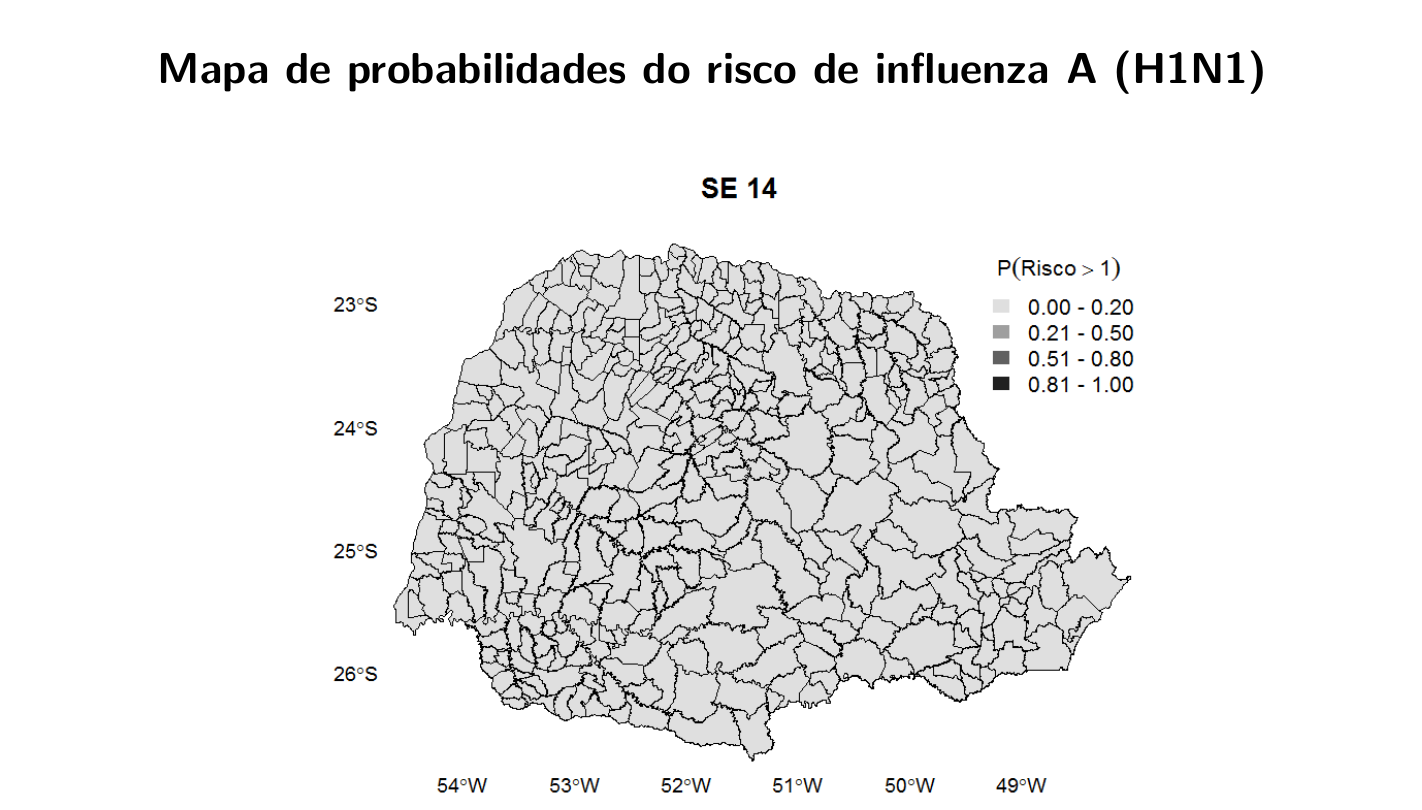
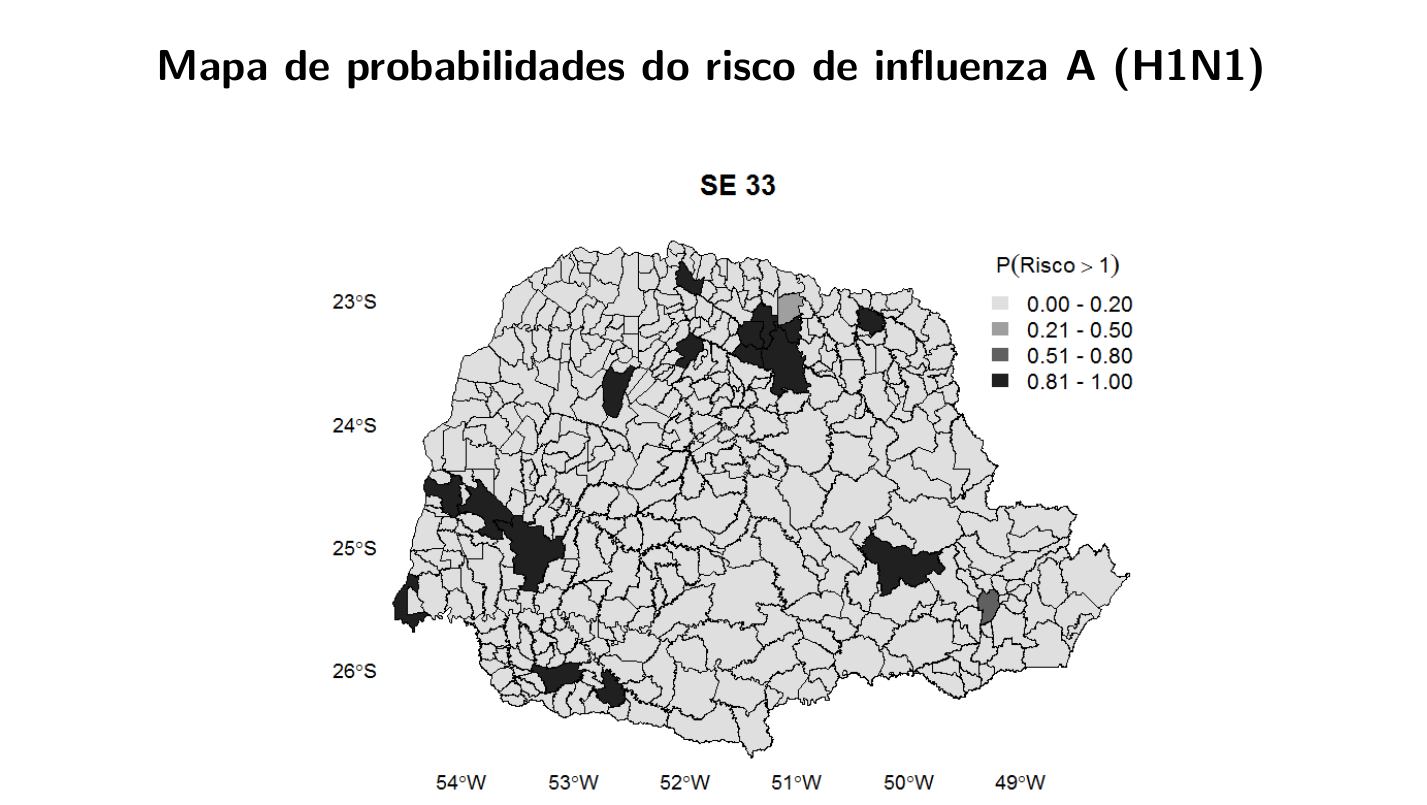
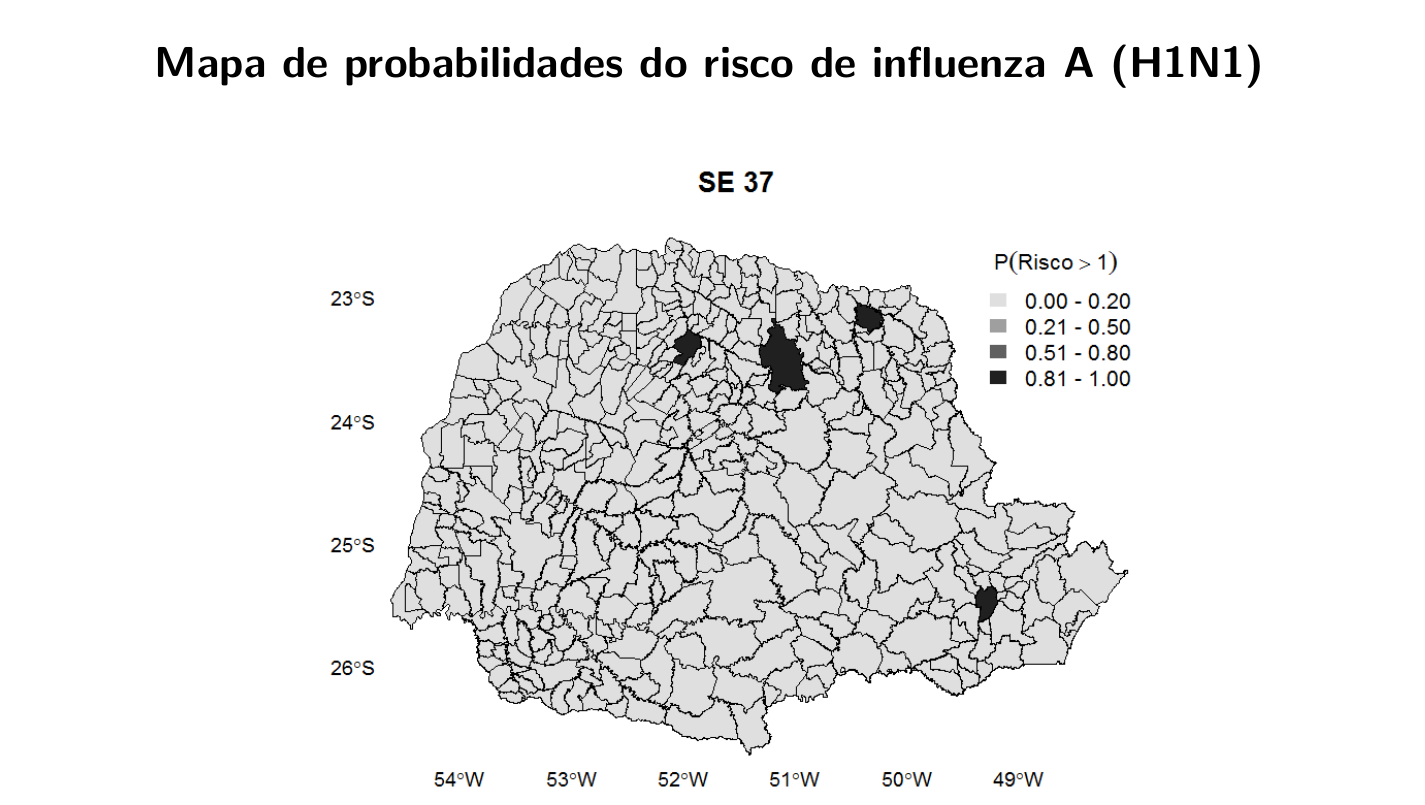
6.15.3 Modelo Espaço-Temporal para a Análise da Morbimortalidade por Influenza
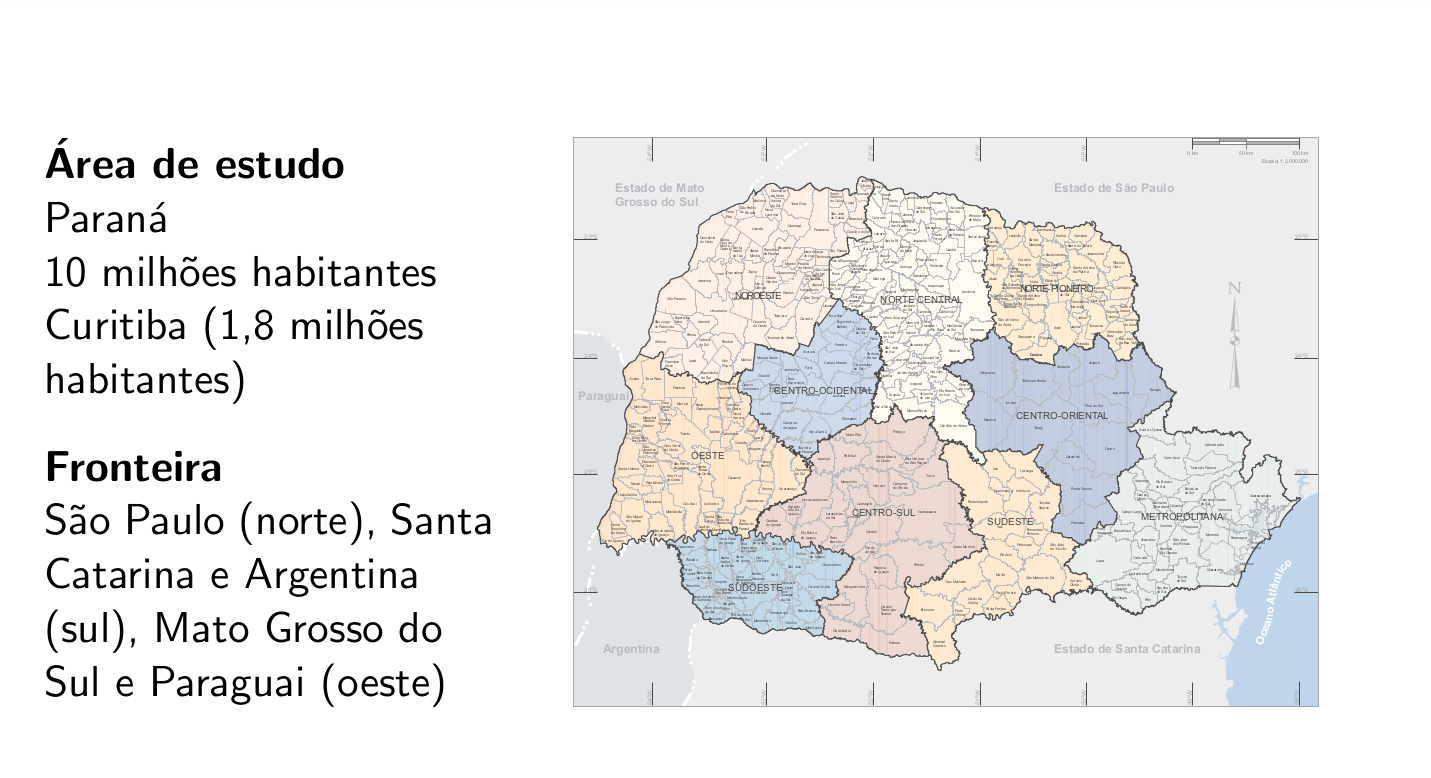
Fonte de dados: Sistema Nacional de Informação de Agravos de Notificação (SINAN) do Ministério da Saúde, Brasil.
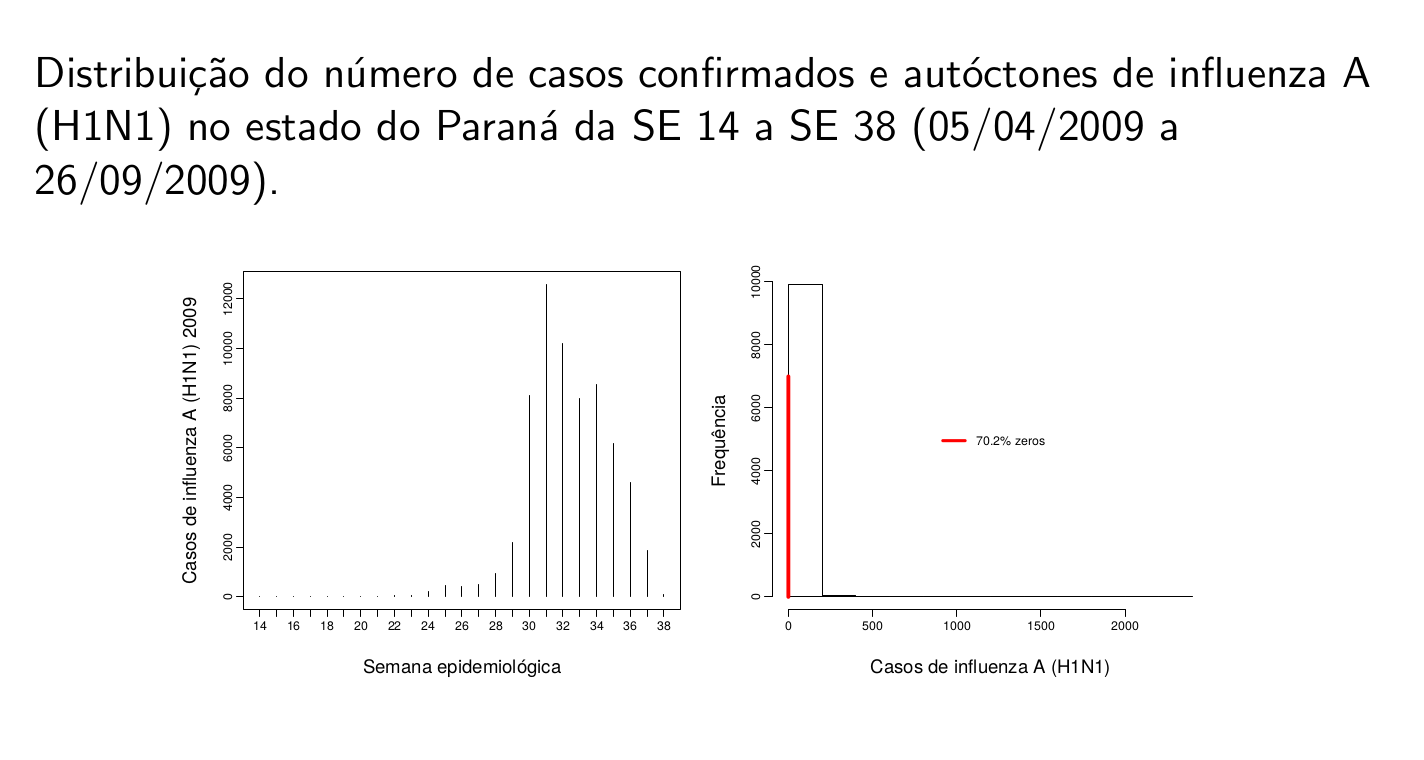
Desfecho: Casos confirmados e autóctones de influenza A (H1N1) de 5 de abril a 26 de setembro de 2009.
Nı́vel de agregação espacial: Município de residência (399)
Nı́vel de agregação temporal: Semana epidemiológica (25)
Covariáveis: Precipitação, temperatura (mı́nima e máxima), umidade relativa do ar, altitude, taxa de pobreza, IDH municipal, densidade demográfica e presença dos principais meios de transporte (ônibus municipal, ônibus intermunicipal, barco e avião).
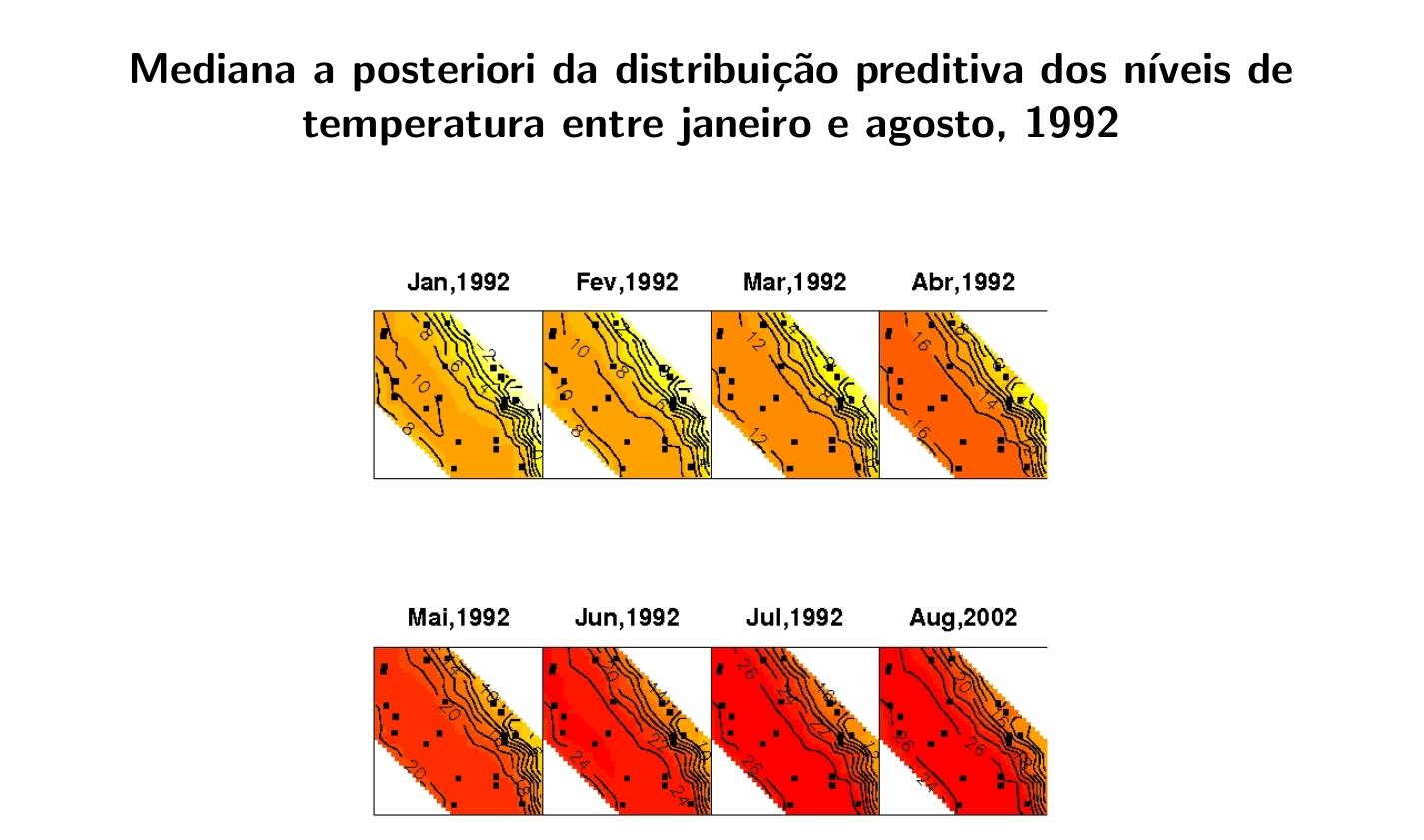
6.15.4 Análise da temperatura na costa central da Califórnia
Os dados consistem de medidas mensais de temperatura em graus centı́grados em 23 estações monitoradoras localizadas na 5 a Região Climática da Califórnia.
As séries temporais correspondem ao perı́odo de janeiro de 1992 a dezembro de 2002.
A altitude para cada uma das estações também estava disponı́vel.
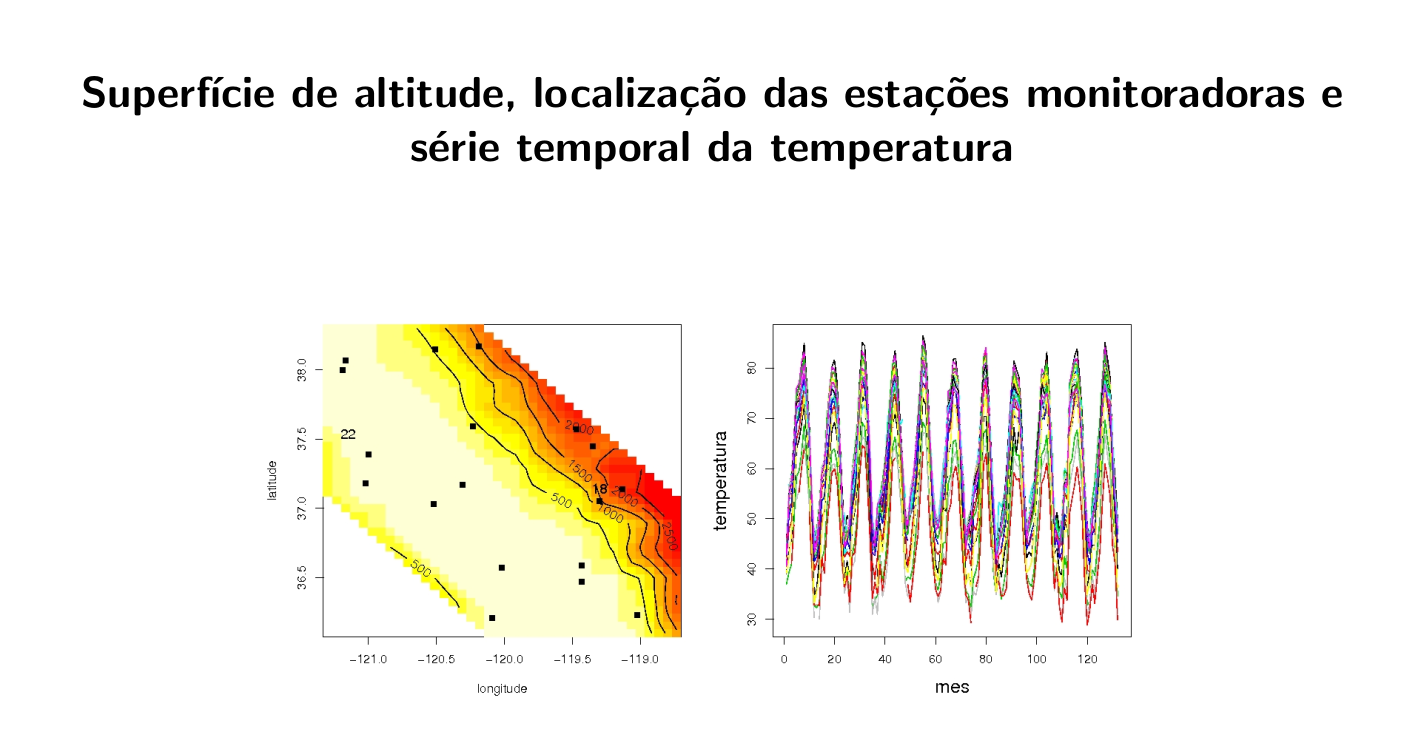
A estrutura de média foi modelada usando um nı́vel variando ao longo do tempo, uma componente sazonal e um termo linear para a altitude.
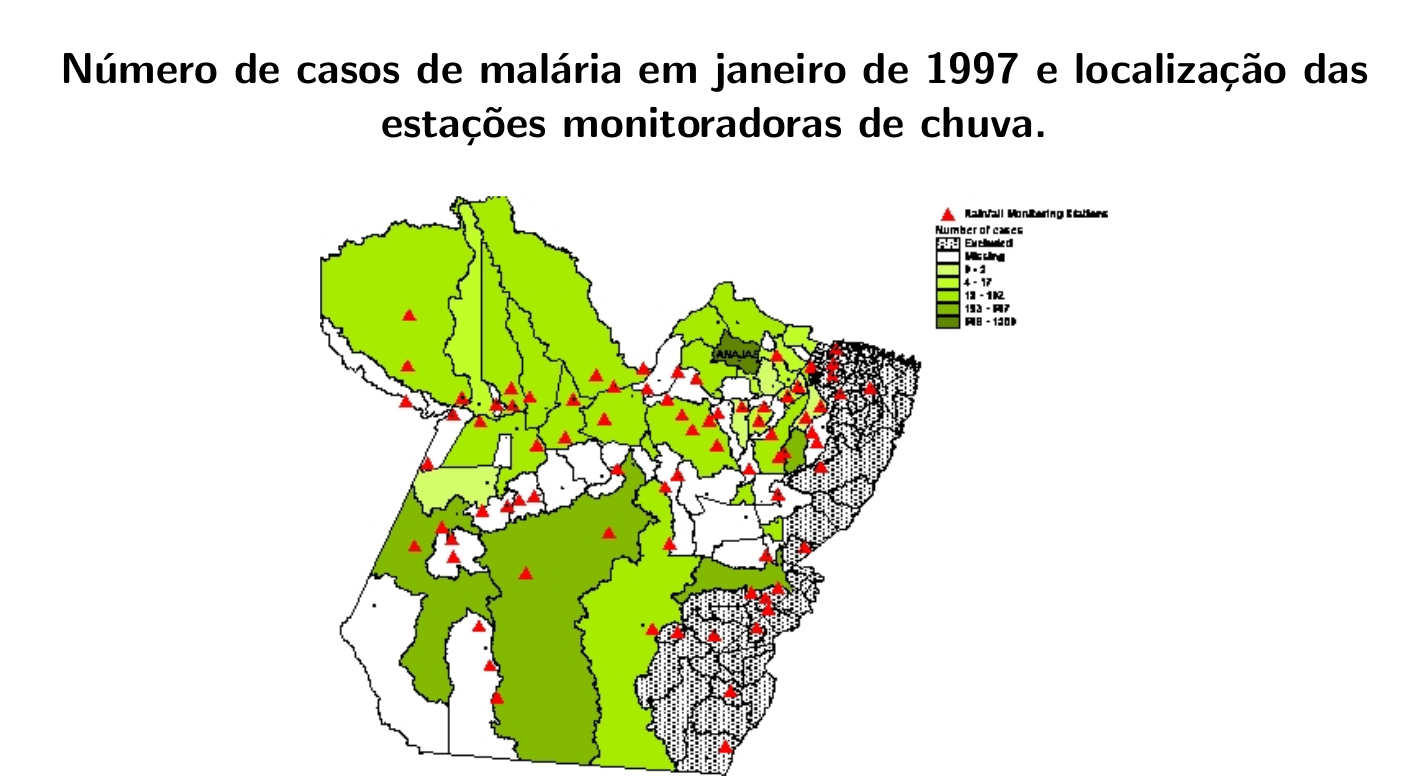
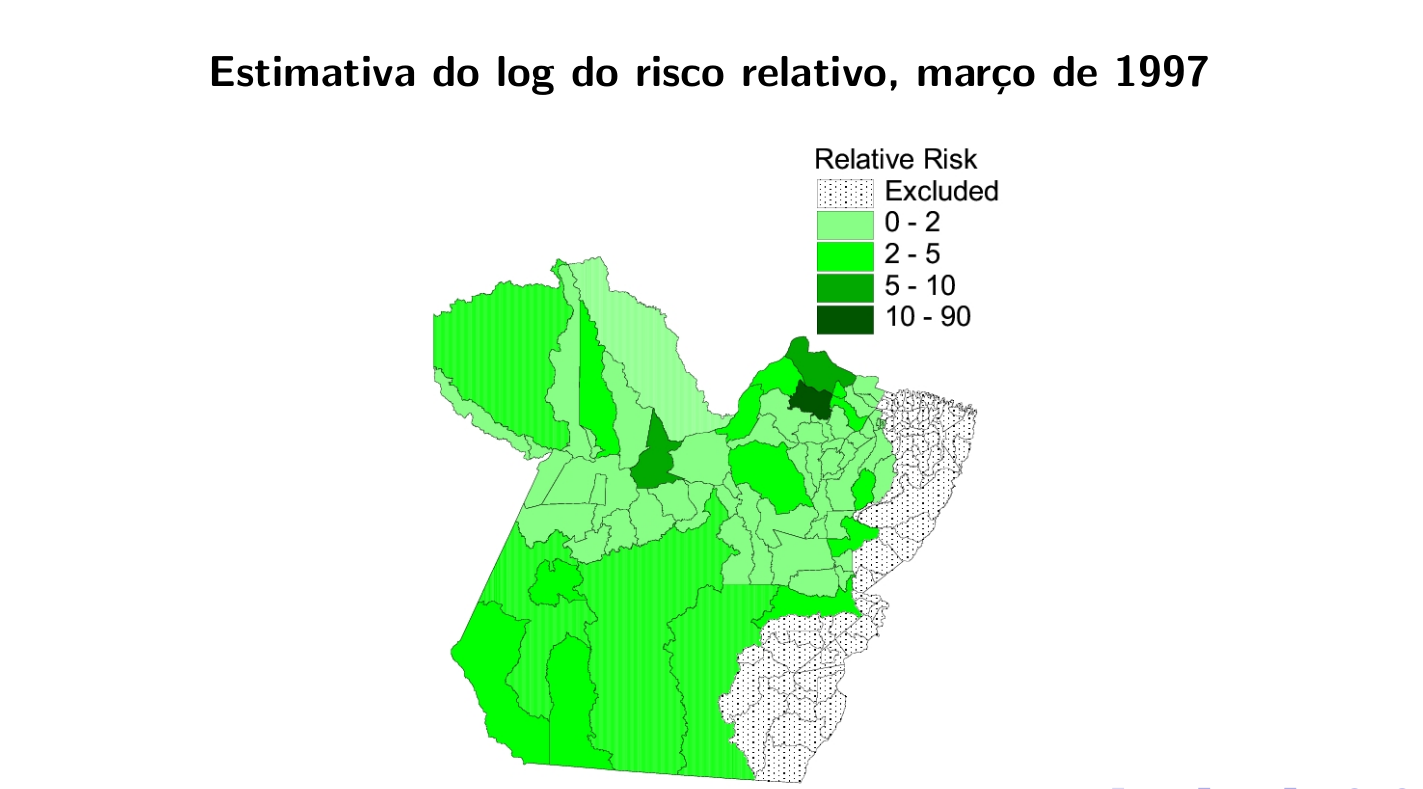
6.15.5 A Relação entre a Malária e a Chuva no Estado do Pará: Uma Análise Espaço-Temporal.
Objetivos:
Estudar as similaridades/diferenças entre as ocorrências de malária no Pará;
Estudar a relação entre a incidência de malária e a quantidade de chuva;
Verificar existência de estrutura espacial e temporal.
Material:
As informações deste trabalho referem-se ao número de casos de malária em alguns municı́pios do estado do Pará através de dados mensais coletados durante os anos de 96 à 98.
Os dados de chuva são dados mensais observados durante os anos de 96 a 98 coletados em 78 estações monitoradoras espalhadas pelos municı́pios.
6.16 Material on line sobre Estatística Espacial
Análise Espacial de Dados Geográficos
http://www.dpi.inpe.br/gilberto/livro/analise/
R Spatial
Geocomputation with R
https://bookdown.org/robinlovelace/geocompr/
Spatial Data Science With Applications in R
6.17 Onde encontrar dados espaciais ?
6.18 Exemplo I: Malhas no R com geobr
O pacote geobr desenvolvido pelo IPEA facilita a obtenção de malhas de estados, municípios e outras regionalizações diretamente no R. Vamos demonstrar um breve exemplo de suas funcionalidades.
library(tidyverse)
# Caso geobr não esteja instalado, rodar:
# install.packages('geobr')
library(geobr)6.18.0.1 Malha de municípios: Estado de São Paulo
As principais funções do pacote geobr para obtenção de malhas têm o prefixo “read_”. Em seguida, especificamos o nível de agregação que desejamos, como por exemplo: unidades da federação (read_state()), municípios (read_municipality()), ou bairros (read_neighborhood).
Neste primeiro exemplo, vamos recuperar a malha dos municípios do estado de São Paulo:
E assim, obtemos o seguinte objeto:
## Simple feature collection with 6 features and 4 fields
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: -51.18 ymin: -23.04 xmax: -46.55 ymax: -21.2
## Geodetic CRS: SIRGAS 2000
## code_muni name_muni code_state abbrev_state geom
## 1 3500105 Adamantina 35 SP MULTIPOLYGON (((-51.09 -21....
## 2 3500204 Adolfo 35 SP MULTIPOLYGON (((-49.7 -21.3...
## 3 3500303 Aguaí 35 SP MULTIPOLYGON (((-47.01 -22....
## 4 3500402 Águas Da Prata 35 SP MULTIPOLYGON (((-46.73 -21....
## 5 3500501 Águas De Lindóia 35 SP MULTIPOLYGON (((-46.63 -22....
## 6 3500550 Águas De Santa Bárbara 35 SP MULTIPOLYGON (((-49.29 -22....Note a coluna geom; é ela que contém as informações sobre a geometria dos municípios.
Para visualizar podemos usar a função nativa plot(), mas também podemos usar o ggplot2, com a função geom_sf()
ggplot(malha_sp) +
geom_sf(aes(geometry=geom)) + # especificamos a coluna referente à geometria
theme_void() # para gerar um gráfico limpo, sem os eixos
6.18.0.2 Malha de bairros: Rio de Janeiro
Agora vamos realizar o mesmo procedimento, mas com um nível de agregação menor: bairros. Podemos obter dados nesse nível utilizando agora a função read_neighborhood. Essa função não permite um filtro de localidade diretamente na chamada da função; assim temos que recuperar a malha de bairros do Brasil inteiro para posteriormente realizar o filtro desejado:
malha_rio <- read_neighborhood() %>%
filter(name_muni == "Rio De Janeiro") # filtrando apenas o município do Rio## Simple feature collection with 6 features and 11 fields
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: -43.27 ymin: -22.96 xmax: -43.17 ymax: -22.91
## Geodetic CRS: SIRGAS 2000
## code_muni name_muni name_neighborhood code_neighborhood code_subdistrict name_subdistrict code_district name_district code_state abbrev_state reference_geom geom
## 1 3304557 Rio De Janeiro Catumbi 330455705005 33045570508 Rio Comprido 330455705 Rio De Janeiro 33 RJ neighborhood MULTIPOLYGON (((-43.2 -22.9...
## 2 3304557 Rio De Janeiro Botafogo 330455705014 33045570509 Botafogo 330455705 Rio De Janeiro 33 RJ neighborhood MULTIPOLYGON (((-43.17 -22....
## 3 3304557 Rio De Janeiro Tijuca 330455705030 33045570513 Tijuca 330455705 Rio De Janeiro 33 RJ neighborhood MULTIPOLYGON (((-43.26 -22....
## 4 3304557 Rio De Janeiro Cosme Velho 330455705013 33045570509 Botafogo 330455705 Rio De Janeiro 33 RJ neighborhood MULTIPOLYGON (((-43.2 -22.9...
## 5 3304557 Rio De Janeiro Flamengo 330455705009 33045570509 Botafogo 330455705 Rio De Janeiro 33 RJ neighborhood MULTIPOLYGON (((-43.18 -22....
## 6 3304557 Rio De Janeiro Glória 330455705010 33045570509 Botafogo 330455705 Rio De Janeiro 33 RJ neighborhood MULTIPOLYGON (((-43.18 -22....Repetimos o código usado anteriormente; a coluna geom agora refere-se aos limites dos bairros.
Nos capítulos referentes à análise de dados de área outras funções serão exploradas.
6.19 Exemplo II: Geocodificação
Há diversas formas de realizar o processo de geocodificação dentro e fora do R. O pacote tidygeocoder permite o envio de um data frame de endereços no R e retorna um objeto tibble com os resultados da geocodificação. O pacote permite a escolha do servidor de preferência - OpenStreetMap, ArcGIS, Bing, Google (Requer API) e outros.
Vamos criar um objeto tibble (equivalente ao data frame, no universo tidyverse) com alguns pontos no Rio de Janeiro:
enderecos <- tribble(~local, ~endereco, "ENSP", "R. Leopoldo Bulhões, 1480 - Manguinhos, Rio de Janeiro - RJ",
"UPA Engenho Novo", "Rua Sousa Barros, 70 - Engenho Novo, Rio de Janeiro - RJ",
"Endereço sem bairro", "Av. de Santa Cruz, 7138, Rio de Janeiro - RJ",
"Praia de Sepetiba", "Praia de Sepetiba, Rio de Janeiro - RJ")
enderecos_cod <- enderecos %>%
geocode(endereco, method = "osm", lat = latitude,
long = longitude)Conferindo o resultado da solicitação:
## # A tibble: 4 × 4
## local endereco latitude longitude
## <chr> <chr> <dbl> <dbl>
## 1 ENSP R. Leopoldo Bulhões, 1480 - Manguinhos, Rio de Janeiro - RJ -22.9 -43.3
## 2 UPA Engenho Novo Rua Sousa Barros, 70 - Engenho Novo, Rio de Janeiro - RJ NA NA
## 3 Endereço sem bairro Av. de Santa Cruz, 7138, Rio de Janeiro - RJ -22.9 -43.5
## 4 Praia de Sepetiba Praia de Sepetiba, Rio de Janeiro - RJ -23.0 -43.7Vê-se que nem todos os endereços foram encontrados utilizando o OpenStreetMap. Vamos visualizar os pontos obtidos junto aos bairros do Rio de Janeiro obtidos anteriormente:
ggplot(enderecos_cod) + geom_sf(data = malha_rio, aes(geometry = geom)) +
geom_point(aes(longitude, latitude), color = "black") +
geom_label(aes(longitude, latitude, label = local),
nudge_y = -0.018) + theme_void()
6.20 Bibliografia sugerida
Bailey, Trevor C.; Gatrell, Anthony C. (1995) Interactive Spatial Data Analysis. Harlow Essex: Longman.
Cressie, N. A. C. (1991). Statistic for Spatial Data. New York.
Costa, Ana C. C., et al. (2015). Surveillance of dengue vectors using spatio-temporal Bayesian modeling. BMC medical informatics and decision making 15.1: 93.
Sansó, B., Schmidt, A. M. e Nobre, A. A. (2008). Bayesian Spatio-temporal models based on discrete convolutions. Canadian Journal of Statistics, 36, 239-258.
Nobre, A. A., Schmidt, A. M. e Lopes, H. F. (2005). Spatio-temporal models for mapping the incidence of malaria in Pará. Environmetrics, 16, 291-304.
Pfeiffer, D. U., et al. (2008) Spatial Analysis in Epidemiology. Oxford University Press.
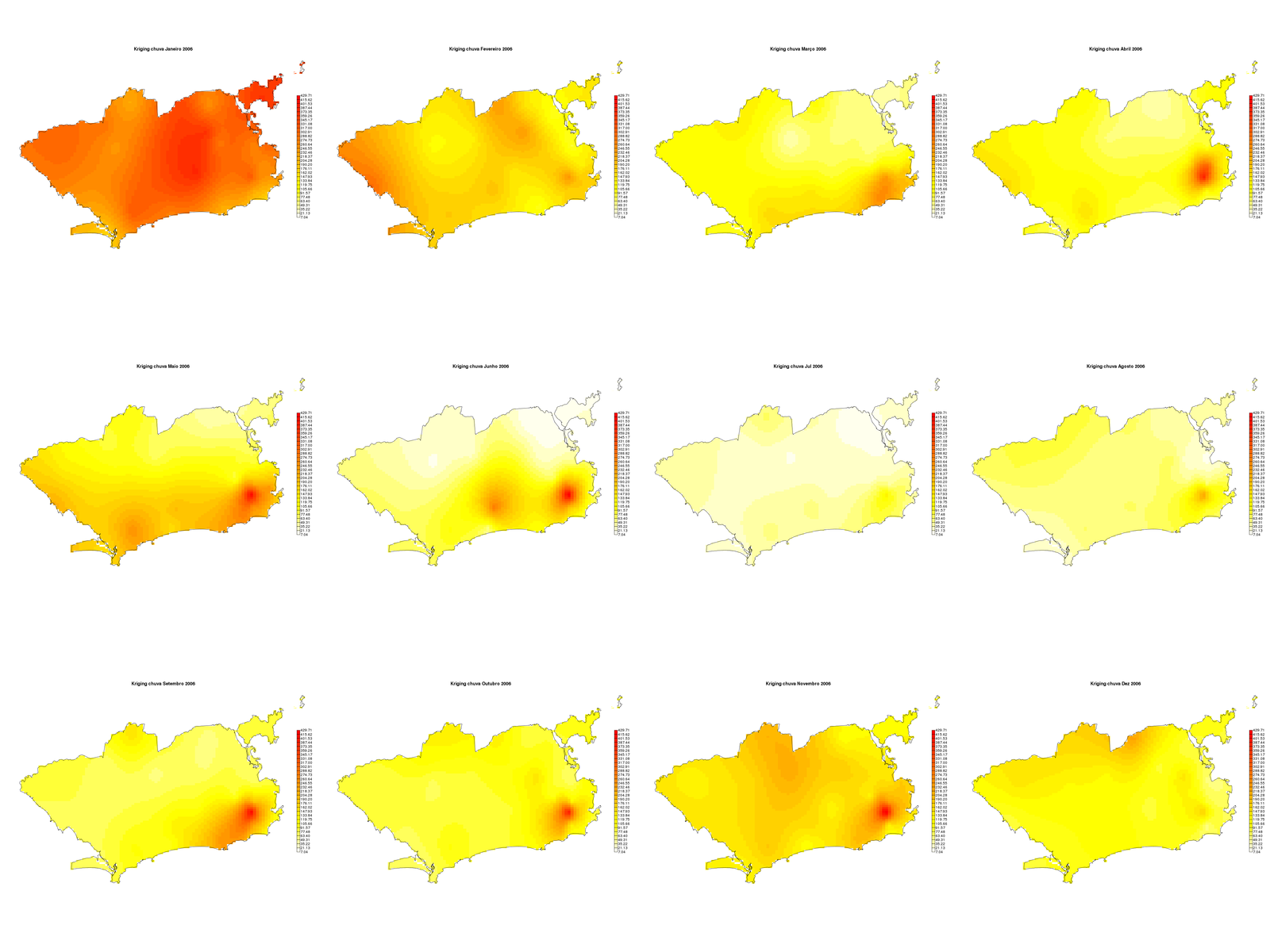

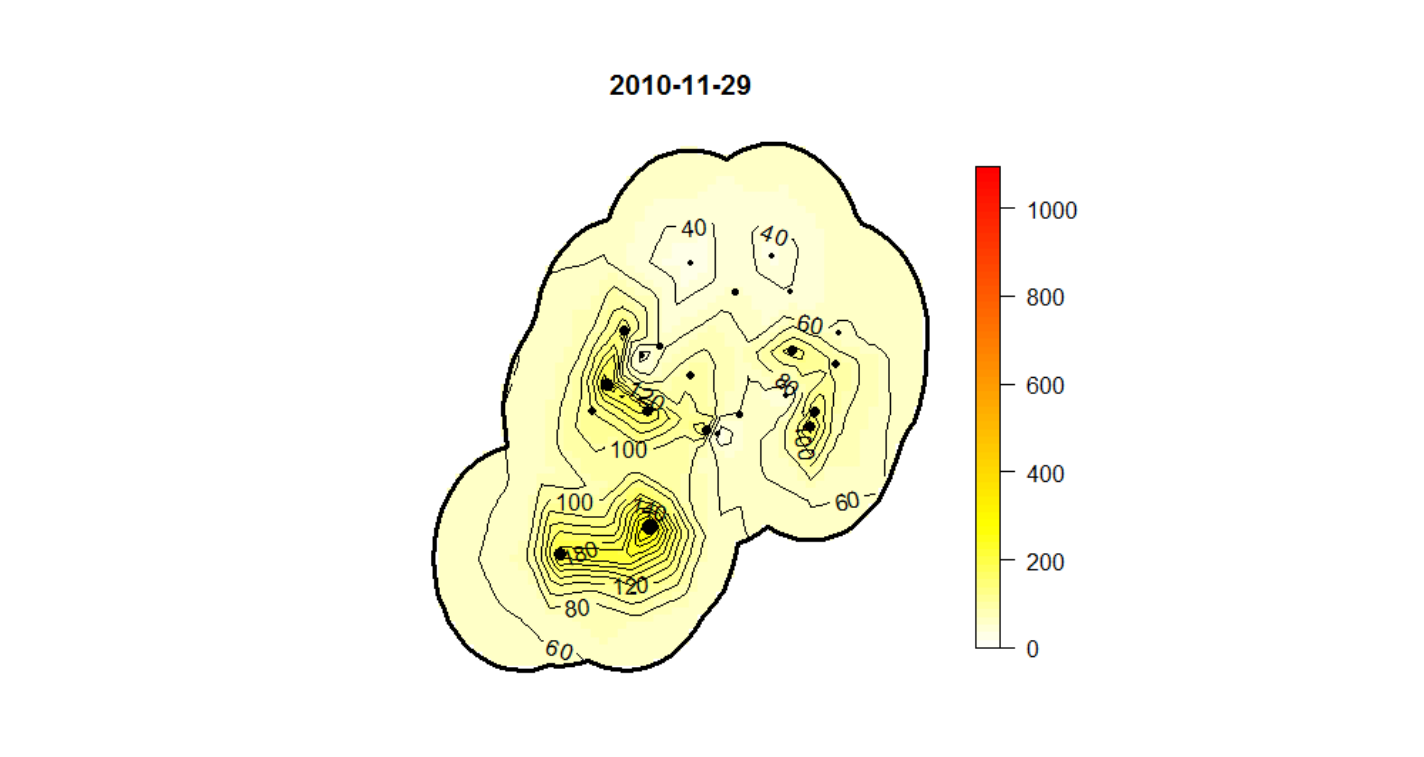
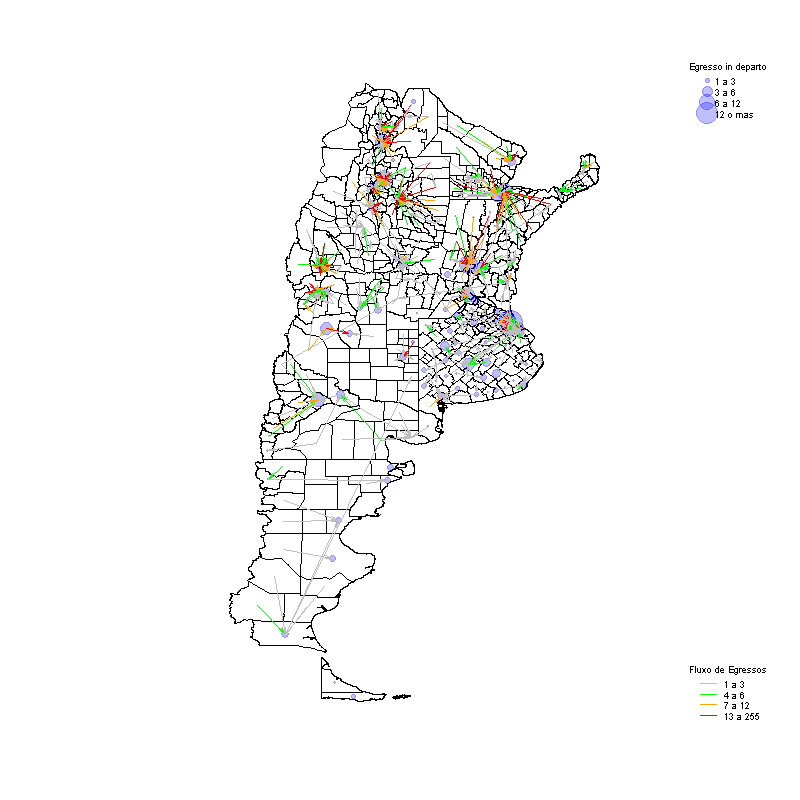
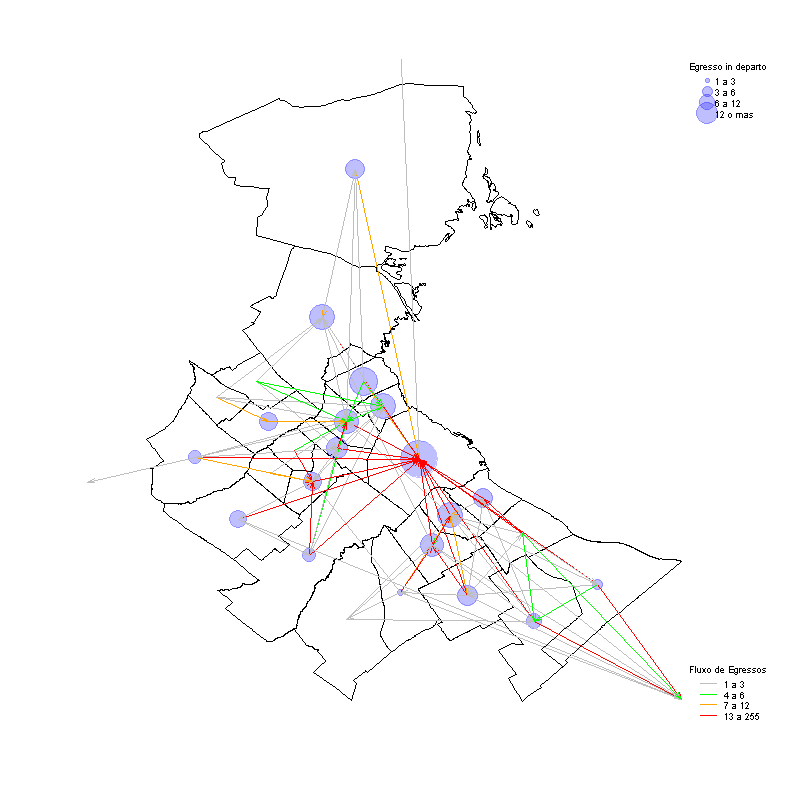 Fonte: Dissertação “Análisis espacial de factores socioeconómicos, de servicios de salud y de mortalidad por cáncer de mama, Argentina, 2009-2011” por Andrea Perinetti.
Fonte: Dissertação “Análisis espacial de factores socioeconómicos, de servicios de salud y de mortalidad por cáncer de mama, Argentina, 2009-2011” por Andrea Perinetti.