10 Dados de Área II

10.1 Modelos de Regressão Espacial

  • Hipótese de independência das observações em geral é Falsa ⇒ Dependência Espacial

  • Efeitos Espaciais ⇒ Se existir forte tendência ou correlação espacial, os resultados serão influenciados, apresentando associação estatı́stica onde não existe (e vice-versa);

  • Como verificar ? ⇒ Medir a autocorrelação espacial dos resı́duos da regressão (Índice de Moran dos resı́duos).

  • Autocorrelação espacial constatada ! E agora ? ⇒ Utilizar Modelos de regressão que incorporam efeitos espaciais:

    • Globais: utilizam um único parâmetro para capturar a estrutura de correlação espacial;

    • Locais: parâmetros variam continuamente no espaço.

10.2 Modelos com Efeitos Espaciais Globais

Suposição: É possı́vel capturar a estrutura de correlação espacial num único parâmetro (adicionado ao modelo de regressão).

Alternativas:

  • Spatial Lag Models (SAR): atribuem a autocorrelação espacial à variável dependente Y

    • Spatial Error Models (CAR): atribuem a autocorrelação ao erro.

10.3 Spatial Lag Models (SAR)

Suposição: A variável \(Y_i\) depende dos valores da variável dependente das áreas vizinhas a \(i\):

\[Y_i = \rho W Y + X\beta + e_i\] Sendo,

  • \(rho\) é o coeficiente espacial auto-regressivo. É a medida de correlação espacial;

    • \(rho = 0\), se a autocorrelação espacial é nula

    • \(W\) É a matriz de vizinhança

10.4 Spatial Error Models (CAR)

Suposição: Os efeitos espaciais estão no ruído:

\[Y = X\beta + e\]

\[ e = \lambda W e + \xi\]

Sendo,

  • \(We\) os erros com efeitos espaciais

    • \(\lambda\) é a medida de correlação espacial

    • \(\xi\) é a componente do erro com variância constante e não correlacionada.

10.5 Modelos SAR vs CAR

  • Motivações diferentes, porém próximas em termos formais;

  • Premissa: processo espacial analisado é estacionário e pode ser capturado em um único parâmetro;

  • Porém isto nem sempre é verdade !

    • Verificar se padrões diversos de associação espacial estão presentes;

    • Indicadores Locais de Autocorrelação Espacial;

    • Resumindo, fazer uma boa análise exploratória de dados espaciais.

10.6 Modelos com Efeitos Espaciais Locais

  • Tais modelos consideram o espaço geográfico heterogêneo ou não-estacionário e a relação entre as variáveis dependentes e independentes assume padrões mais ou menos regionalizados;

  • Os parâmetros estimados podem ser mapeados para examinar as variações locais;

  • Idem para os erros dos parâmetros;

  • Possibilidade de testar, por exemplo, a hipótese da variação dos parâmetros da área de estudo ser ou não aleatória.

Ex:

  • Regressão Geograficamente Ponderada (GWR)

  • Modelos Bayesianos Completo

  • INLA (integrated nested Laplace approximations)

Ex: Vamos modelar espacialmente a taxa de detecção da hanseníase em Olinda/PE.

Antes de mais nada como na aula anterior vamos baixar o ZIP contendo os arquivos no formato shape

Leando o shape file de Olinda/PE.

Fazendo o sumário estatístico da variável taxa.

      AREA           PERIMETER        SETOR_       SETOR_ID        VAR5       DENS_DEMO          SET          CASES            POP           DEPRIV               geometry         tx       
 Min.   :  12817   Min.   : 566   Min.   :  2   Min.   :  1   Min.   :  1   Min.   :  375   Min.   :  1   Min.   : 0.00   Min.   : 337   Min.   :0.007   POLYGON      :241   Min.   :  0.0  
 1st Qu.:  69889   1st Qu.:1306   1st Qu.: 62   1st Qu.: 61   1st Qu.: 63   1st Qu.: 8216   1st Qu.: 63   1st Qu.: 2.00   1st Qu.:1214   1st Qu.:0.199   epsg:5535    :  0   1st Qu.: 13.2  
 Median : 111374   Median :1719   Median :122   Median :121   Median :123   Median :13244   Median :123   Median : 4.00   Median :1411   Median :0.328   +proj=utm ...:  0   Median : 29.2  
 Mean   : 182939   Mean   :1996   Mean   :122   Mean   :122   Mean   :123   Mean   :15042   Mean   :123   Mean   : 5.94   Mean   :1432   Mean   :0.358                       Mean   : 40.9  
 3rd Qu.: 169730   3rd Qu.:2189   3rd Qu.:182   3rd Qu.:182   3rd Qu.:183   3rd Qu.:19671   3rd Qu.:183   3rd Qu.: 8.00   3rd Qu.:1636   3rd Qu.:0.509                       3rd Qu.: 54.1  
 Max.   :2774850   Max.   :8861   Max.   :244   Max.   :245   Max.   :243   Max.   :53619   Max.   :243   Max.   :37.00   Max.   :2764   Max.   :0.907                       Max.   :230.4

Criando a matriz de vizinhaça por contiguidade.

Ajustando o modelo de regressão linear simples.


Call:
lm(formula = tx ~ DEPRIV, data = olinda.sf)

Residuals:
   Min     1Q Median     3Q    Max 
-63.39 -25.33  -9.07  14.82 175.93 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)    19.06       4.93    3.86  0.00014 ***
DEPRIV         60.81      11.92    5.10  6.9e-07 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 38.3 on 239 degrees of freedom
Multiple R-squared:  0.0982,    Adjusted R-squared:  0.0944 
F-statistic:   26 on 1 and 239 DF,  p-value: 6.86e-07

Checando os residuos para verificar a presença de autocorrelação.


    Moran I test under randomisation

data:  olinda.lm$lmresid  
weights: pesos.viz    

Moran I statistic standard deviate = 7.4, p-value = 8e-14
alternative hypothesis: greater
sample estimates:
Moran I statistic       Expectation          Variance 
         0.286742         -0.004167          0.001551

Ajustando o modelo SAR.


Call:spatialreg::lagsarlm(formula = formula, data = data, listw = listw,     na.action = na.action, Durbin = Durbin, type = type, method = method,     quiet = quiet, zero.policy = zero.policy, interval = interval,     tol.solve = tol.solve, trs = trs, control = control)

Residuals:
     Min       1Q   Median       3Q      Max 
-76.4924 -21.4142  -8.9083  14.7660 169.2090 

Type: lag 
Coefficients: (asymptotic standard errors) 
            Estimate Std. Error z value Pr(>|z|)
(Intercept)   8.6655     4.8474  1.7877 0.073831
DEPRIV       31.5886    10.7773  2.9310 0.003378

Rho: 0.4975, LR test value: 44.56, p-value: 2.4701e-11
Asymptotic standard error: 0.07355
    z-value: 6.763, p-value: 1.3471e-11
Wald statistic: 45.74, p-value: 1.3471e-11

Log likelihood: -1197 for lag model
ML residual variance (sigma squared): 1146, (sigma: 33.86)
Number of observations: 241 
Number of parameters estimated: 4 
AIC: 2402, (AIC for lm: 2445)
LM test for residual autocorrelation
test value: 26.86, p-value: 2.1863e-07

Checando os residuos para verificar a presença de autocorrelação.


    Moran I test under randomisation

data:  olinda.sar$lagresid  
weights: pesos.viz    

Moran I statistic standard deviate = -1.5, p-value = 0.9
alternative hypothesis: greater
sample estimates:
Moran I statistic       Expectation          Variance 
        -0.062890         -0.004167          0.001549

Ajustando o modelo CAR.


Call:spatialreg::errorsarlm(formula = formula, data = data, listw = listw,     na.action = na.action, Durbin = Durbin, etype = etype, method = method,     quiet = quiet, zero.policy = zero.policy, interval = interval,     tol.solve = tol.solve, trs = trs, control = control)

Residuals:
     Min       1Q   Median       3Q      Max 
-75.7356 -22.1263  -9.0949  13.2751 171.2697 

Type: error 
Coefficients: (asymptotic standard errors) 
            Estimate Std. Error z value Pr(>|z|)
(Intercept)  30.6921     6.5681  4.6729 2.97e-06
DEPRIV       25.2000    13.3899  1.8820  0.05983

Lambda: 0.5098, LR test value: 39.59, p-value: 3.1416e-10
Asymptotic standard error: 0.07399
    z-value: 6.89, p-value: 5.5955e-12
Wald statistic: 47.47, p-value: 5.5955e-12

Log likelihood: -1200 for error model
ML residual variance (sigma squared): 1167, (sigma: 34.16)
Number of observations: 241 
Number of parameters estimated: 4 
AIC: 2407, (AIC for lm: 2445)

Checando os residuos para verificar a presença de autocorrelação.


    Moran I test under randomisation

data:  olinda.car$carresid  
weights: pesos.viz    

Moran I statistic standard deviate = -1.1, p-value = 0.9
alternative hypothesis: greater
sample estimates:
Moran I statistic       Expectation          Variance 
        -0.048484         -0.004167          0.001548

Mapeando os valores observados e preditos dos modelos ajustados

library(colorspace) # 

olinda.sf$brks <- cut(olinda.sf$tx, include.lowest=TRUE,  right=TRUE,
                   breaks=c(-0.01, 0, 15, 30, 45, 100, 231), 
                   labels=c("0", "0 - 15", "15 - 30", "30 - 45", "45 - 100", "> 100"))

tx.bruta <- ggplot(olinda.sf) + 
  geom_sf(aes(fill = brks), color = 'black') +
  ggtitle("Taxa Bruta") + 
  scale_fill_discrete_sequential(palette ='Heat',  
                                 c1=80,c2 =30,l1=30,l2=90,p1=0.2,p2=1.5,
                                 na.value = "grey75", 
                                 drop=FALSE,
                                 name='Taxa') +
  theme_void()
  
  
 
olinda.sf$brks.lm <- cut(olinda.lm$fitted.values, include.lowest=TRUE,  right=TRUE,
                   breaks=c(-0.01, 0, 15, 30, 45, 100, 231), 
                   labels=c("0", "0 - 15", "15 - 30", "30 - 45", "45 - 100", "> 100"))


tx.lm <- ggplot(olinda.sf) + 
  geom_sf(aes(fill = brks.lm), color = 'black') +
  ggtitle("Taxa Predita - LM") + 
  scale_fill_discrete_sequential(palette ='Heat',  
                                 c1=80,c2 =30,l1=30,l2=90,p1=0.2,p2=1.5,
                                 na.value = "grey75", 
                                 drop=FALSE,
                                 name='Taxa') +
  theme_void()

olinda.sf$brks.sar <- cut(olinda.sar$fitted.values, include.lowest=TRUE,  right=TRUE,
                   breaks=c(-0.01, 0, 15, 30, 45, 100, 231), 
                   labels=c("0", "0 - 15", "15 - 30", "30 - 45", "45 - 100", "> 100"))


tx.sar <- ggplot(olinda.sf) + 
  geom_sf(aes(fill = brks.sar), color = 'black') +
  ggtitle("Taxa Predita - SAR") + 
  scale_fill_discrete_sequential(palette ='Heat', 
                                 c1=80,c2 =30,l1=30,l2=90,p1=0.2,p2=1.5,
                                 na.value = "grey75", 
                                 drop=FALSE,
                                 name='Taxa') +
  theme_void()

olinda.sf$brks.car <- cut(olinda.car$fitted.values, include.lowest=TRUE,  right=TRUE,
                   breaks=c(-0.01, 0, 15, 30, 45, 100, 231), 
                   labels=c("0", "0 - 15", "15 - 30", "30 - 45", "45 - 100", "> 100"))


tx.car <- ggplot(olinda.sf) + 
  geom_sf(aes(fill = brks.car), color = 'black') +
  ggtitle("Taxa Predita - CAR") + 
  scale_fill_discrete_sequential(palette ='Heat', 
                                 c1=80,c2 =30,l1=30,l2=90,p1=0.2,p2=1.5,
                                 na.value = "grey75", 
                                 drop=FALSE,
                                 name='Taxa') +
  theme_void()


library(gridExtra)
grid.arrange(tx.bruta, tx.lm, tx.sar, tx.car, ncol=2)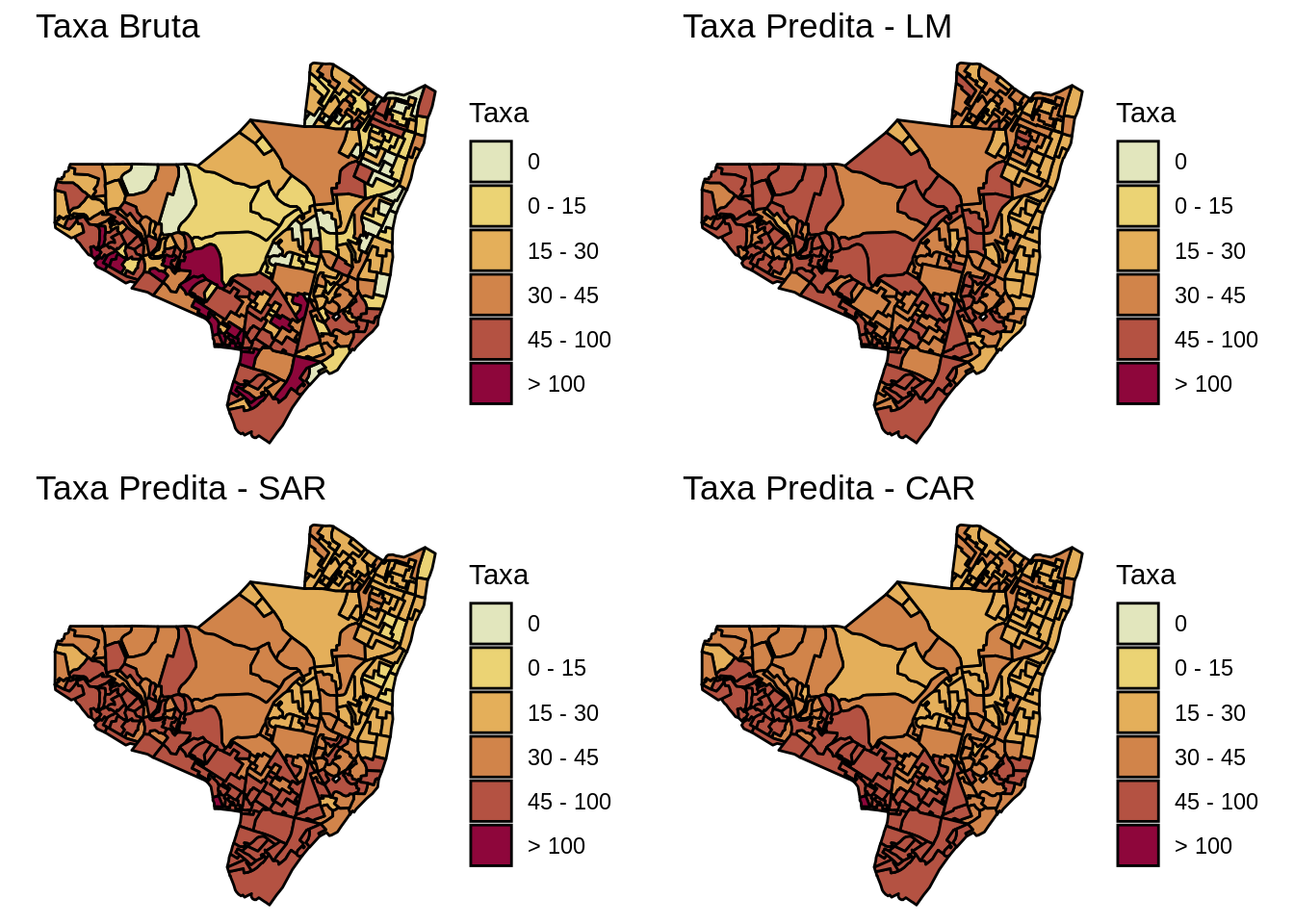

Verificando a distribuição dos resíduos.

[1] -76.49 175.93

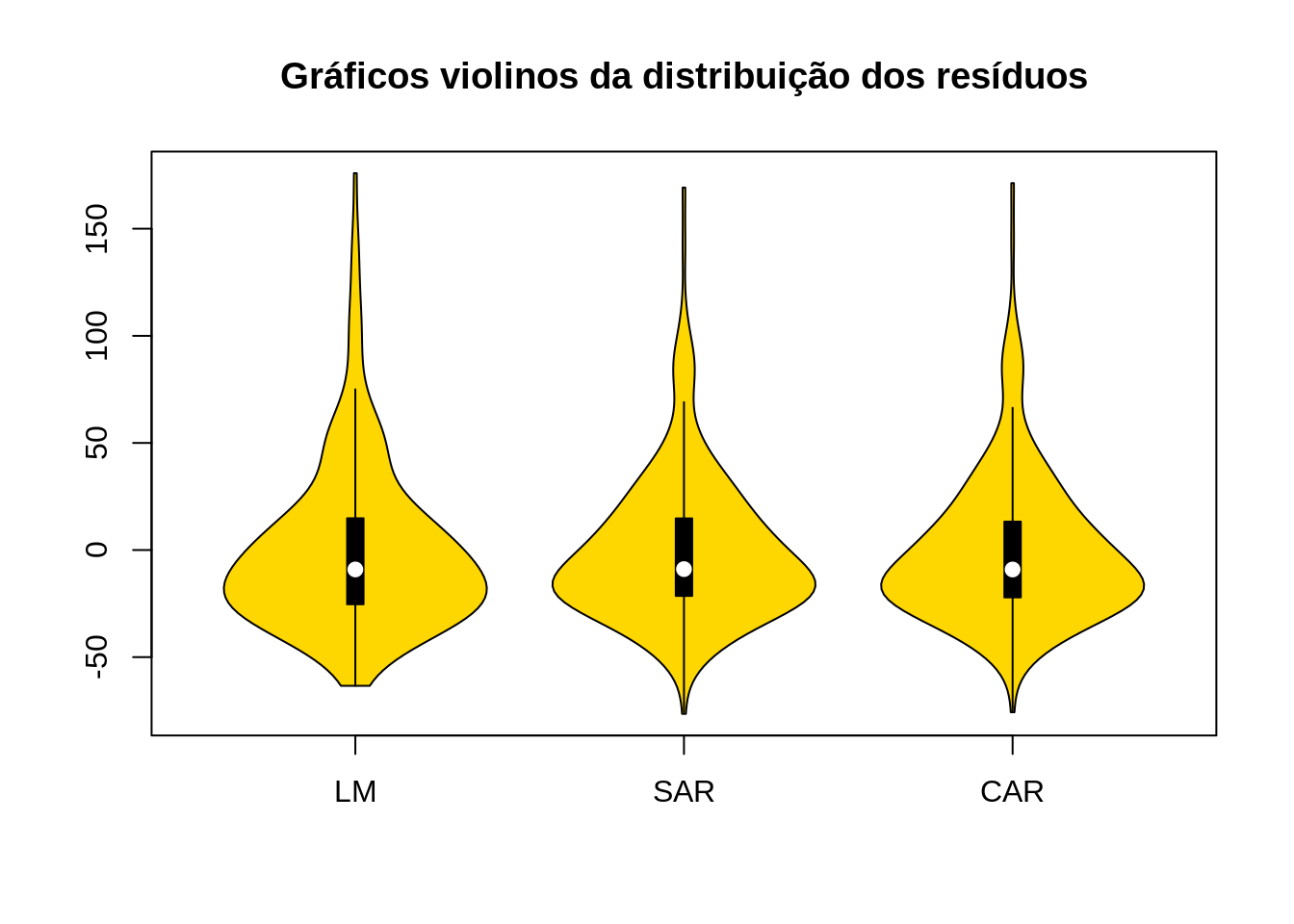
Mapeando a distribuição dos resíduos.

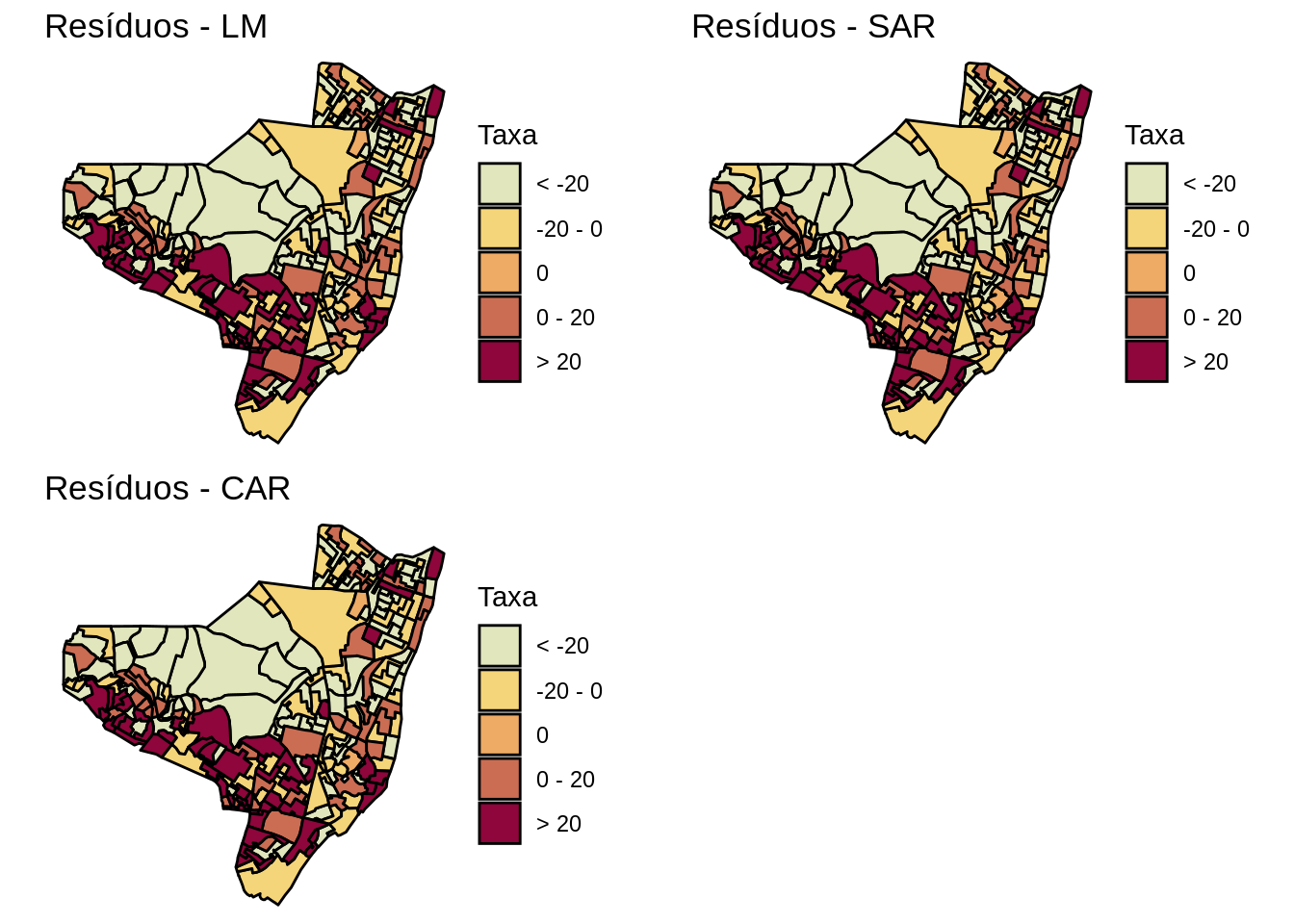
10.7 Modelos com Efeitos Espaciais Locais

Regressão Geograficamente Ponderada (GWR): Ajusta um modelo de regressão a cada ponto observado, ponderando todas as demais observações como função da distância deste ponto;

\[Y(s) = \beta(s)X+e\]

Sabendo que:

  • \(Y(s)\): É a variável que representa o processo no ponto \(s\);

  • \(\beta\): São os parâmetros estimados no ponto \(s\);

  • Para estimar os parâmetros desse modelo, a solução é o uso de um estimador baseado em mínimos quadrados generalizado por algum métodos de ajuste local (ex: kernel);

\[\beta(s) = (X^T W(s) X)^{-1}X^T W(s)Y\]

  • O ajuste local é feito de forma a garantir uma influência maior dos pontos mais próximos (como o kernel);

  • Valor da largura de banda;

  • As duas funções mais usadas para o cálculo dos pesos é a “bi-square” e a “gaussiana”;

  • Tais modelos consideram o espaço geográfico heterogêneo ou não-estacionário e a relação entre as variáveis dependentes e independentes assume padrões mais ou menos regionalizados;

  • Os parâmetros estimados podem ser mapeados para examinar as variações locais;

  • Idem para os erros dos parâmetros;

  • Possibilidade de testar, por exemplo, a hipótese da variação dos parâmetros da área de estudo ser ou não aleatória;

  • O método GWR permite a realização de estudos de fenômenos com diferentes nı́veis de heterogeneidade espacial;

  • Mapeamentos de diagnóstico e dos parâmetros permitem novas interpretações e insights de padrões espaciais.

Ex: Vamos modelar a taxa de detecção de hanseníase em Olinada/PE utilizando um modelo GWR.

Primeiramente vamos transformar os centroides dos setores censitários em formato sp, pois iremnos precisar das colunas referentes as coordenadas.

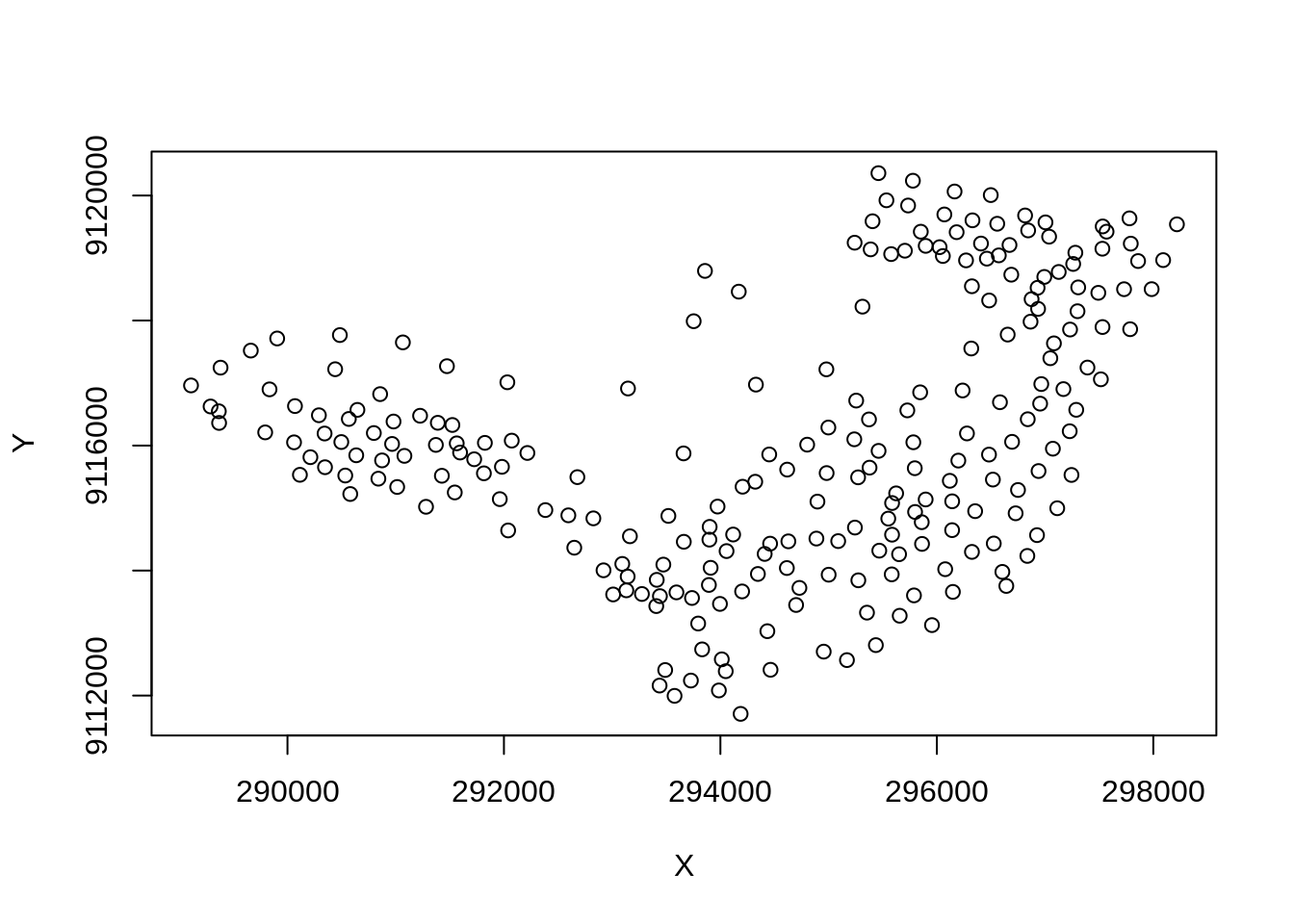
Precisamos estimar a largura de banda “ideal” para o kernel

Adaptive q: 0.382 CV score: 317689 
Adaptive q: 0.618 CV score: 333605 
Adaptive q: 0.2361 CV score: 296459 
Adaptive q: 0.1459 CV score: 279322 
Adaptive q: 0.09017 CV score: 269226 
Adaptive q: 0.05573 CV score: 260430 
Adaptive q: 0.03444 CV score: 256832 
Adaptive q: 0.02129 CV score: 261631 
Adaptive q: 0.03963 CV score: 255671 
Adaptive q: 0.04162 CV score: 255356 
Adaptive q: 0.04701 CV score: 257702 
Adaptive q: 0.04368 CV score: 256161 
Adaptive q: 0.04121 CV score: 255348 
Adaptive q: 0.04134 CV score: 255331 
Adaptive q: 0.0414 CV score: 255323 
Adaptive q: 0.04148 CV score: 255312 
Adaptive q: 0.04154 CV score: 255326 
Adaptive q: 0.04144 CV score: 255317 
Adaptive q: 0.04148 CV score: 255312 
[1] 0.04148

Ajustando o modelo GWR

Call:
gwr(formula = tx ~ DEPRIV, data = olinda.sf, coords = cbind(centroides.sp$X, 
    centroides.sp$Y), adapt = GWRbanda, hatmatrix = TRUE, se.fit = TRUE)
Kernel function: gwr.Gauss 
Adaptive quantile: 0.04148 (about 9 of 241 data points)
Summary of GWR coefficient estimates at data points:
               Min. 1st Qu. Median 3rd Qu.   Max. Global
X.Intercept.   6.23   20.51  32.73   46.75  94.12   19.1
DEPRIV       -49.77   -8.64  15.11   31.96 100.19   60.8
Number of data points: 241 
Effective number of parameters (residual: 2traceS - traceS'S): 33.78 
Effective degrees of freedom (residual: 2traceS - traceS'S): 207.2 
Sigma (residual: 2traceS - traceS'S): 32.03 
Effective number of parameters (model: traceS): 24.11 
Effective degrees of freedom (model: traceS): 216.9 
Sigma (model: traceS): 31.3 
Sigma (ML): 29.7 
AICc (GWR p. 61, eq 2.33; p. 96, eq. 4.21): 2375 
AIC (GWR p. 96, eq. 4.22): 2343 
Residual sum of squares: 212532 
Quasi-global R2: 0.4532

Colocando a saída do modelo dentro de um dataframe.

  sum.w X.Intercept. DEPRIV X.Intercept._se DEPRIV_se   gwr.e  pred pred.se localR2 X.Intercept._se_EDF DEPRIV_se_EDF pred.se.1 coord.x coord.y
1 19.33        29.75 -36.58           10.66     38.47  14.995 14.68   8.464  0.1864               10.91         39.36     8.659  295460 9120358
2 17.44        32.35 -44.33           12.16     43.38  13.805 24.90   6.684  0.1933               12.44         44.38     6.839  295779 9120237
3 17.20        34.14 -49.45           12.39     42.78   4.575 24.65   6.360  0.1766               12.67         43.76     6.507  296164 9120064
4 16.51        31.31 -43.95           12.87     45.91  -4.908 10.57  11.935  0.2109               13.16         46.97    12.210  295534 9119924
5 15.27        32.60 -48.49           13.72     48.56 -11.850 17.95   6.766  0.2161               14.04         49.68     6.922  295734 9119840
6 19.08        33.43 -46.53           11.15     37.99   6.203 28.92   8.094  0.1523               11.41         38.87     8.281  296498 9120007

Verificando a distribuição dos coeficientes de regressão para a variável DEPRIVED

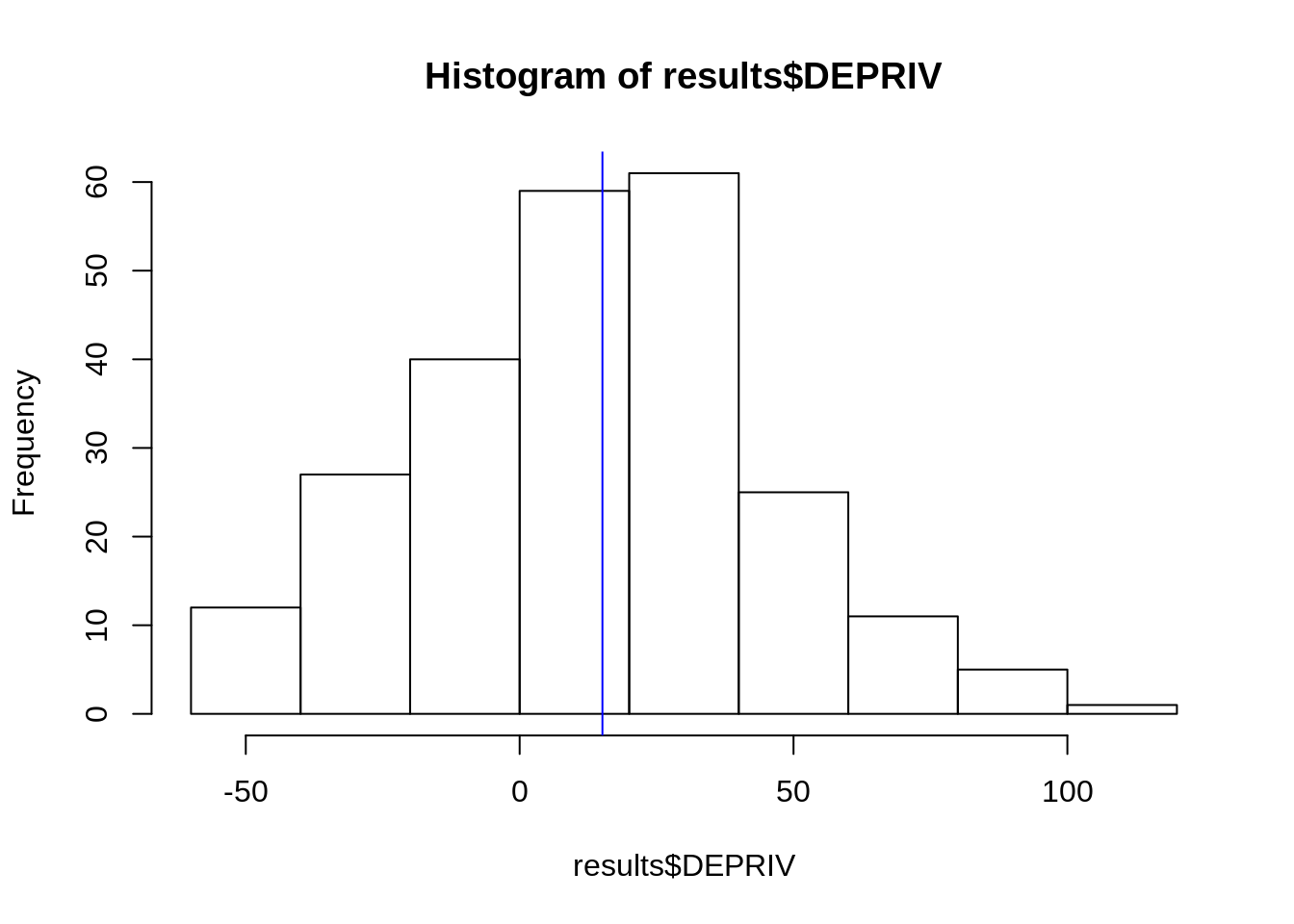
Verificando a distribuição dos localR2

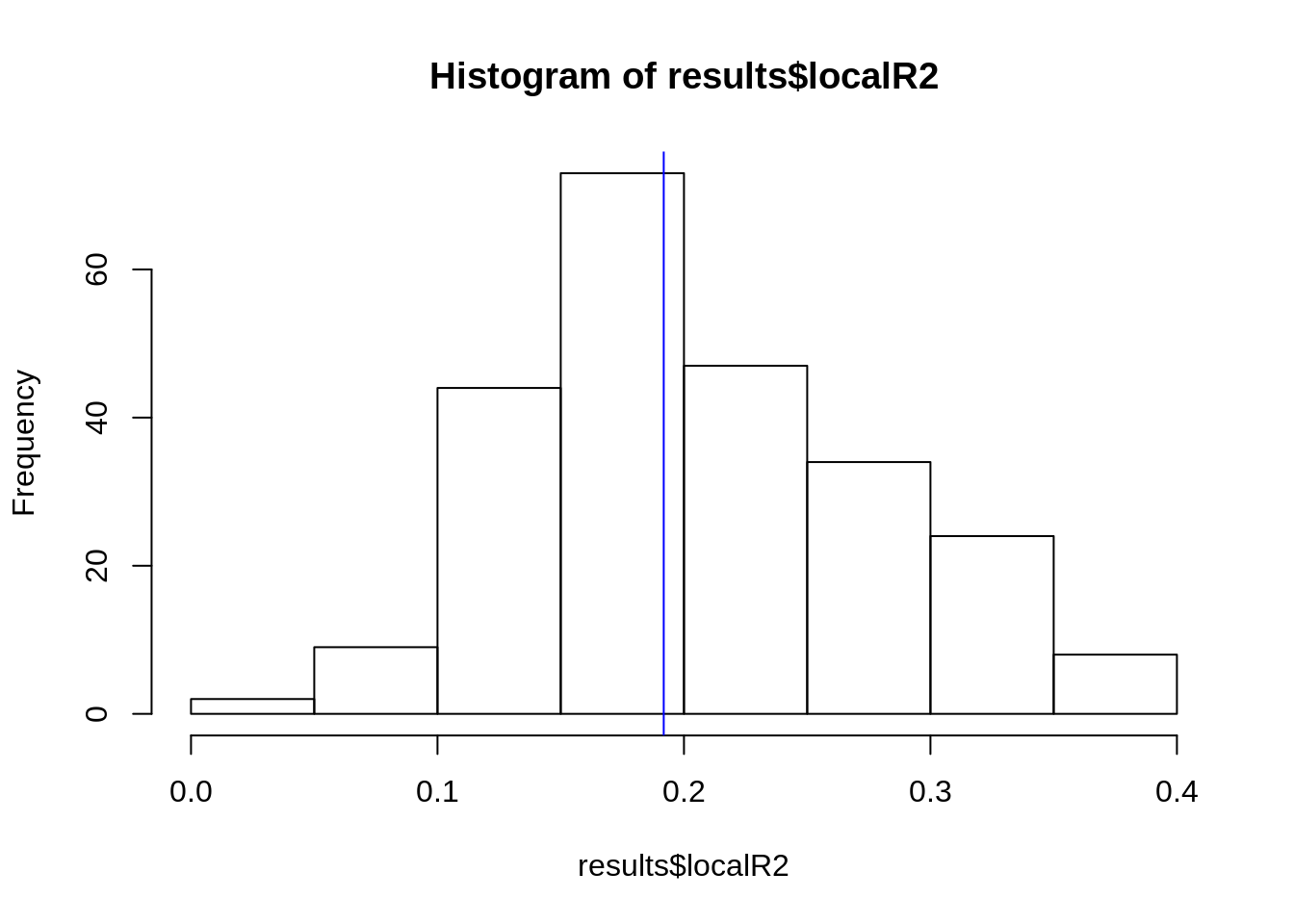
Incorporando alguns parâmetros de saída do modelo na tabela olinda.sf

Definindo as paletes de cores para a construção dos mapas.

 [1] "BottleRocket1"  "BottleRocket2"  "Rushmore1"      "Rushmore"       "Royal1"         "Royal2"         "Zissou1"        "Darjeeling1"    "Darjeeling2"    "Chevalier1"     "FantasticFox1"  "Moonrise1"      "Moonrise2"      "Moonrise3"      "Cavalcanti1"    "GrandBudapest1" "GrandBudapest2" "IsleofDogs1"    "IsleofDogs2"

Mapa dos coeficientes de regressão para a variável DEPRIVED

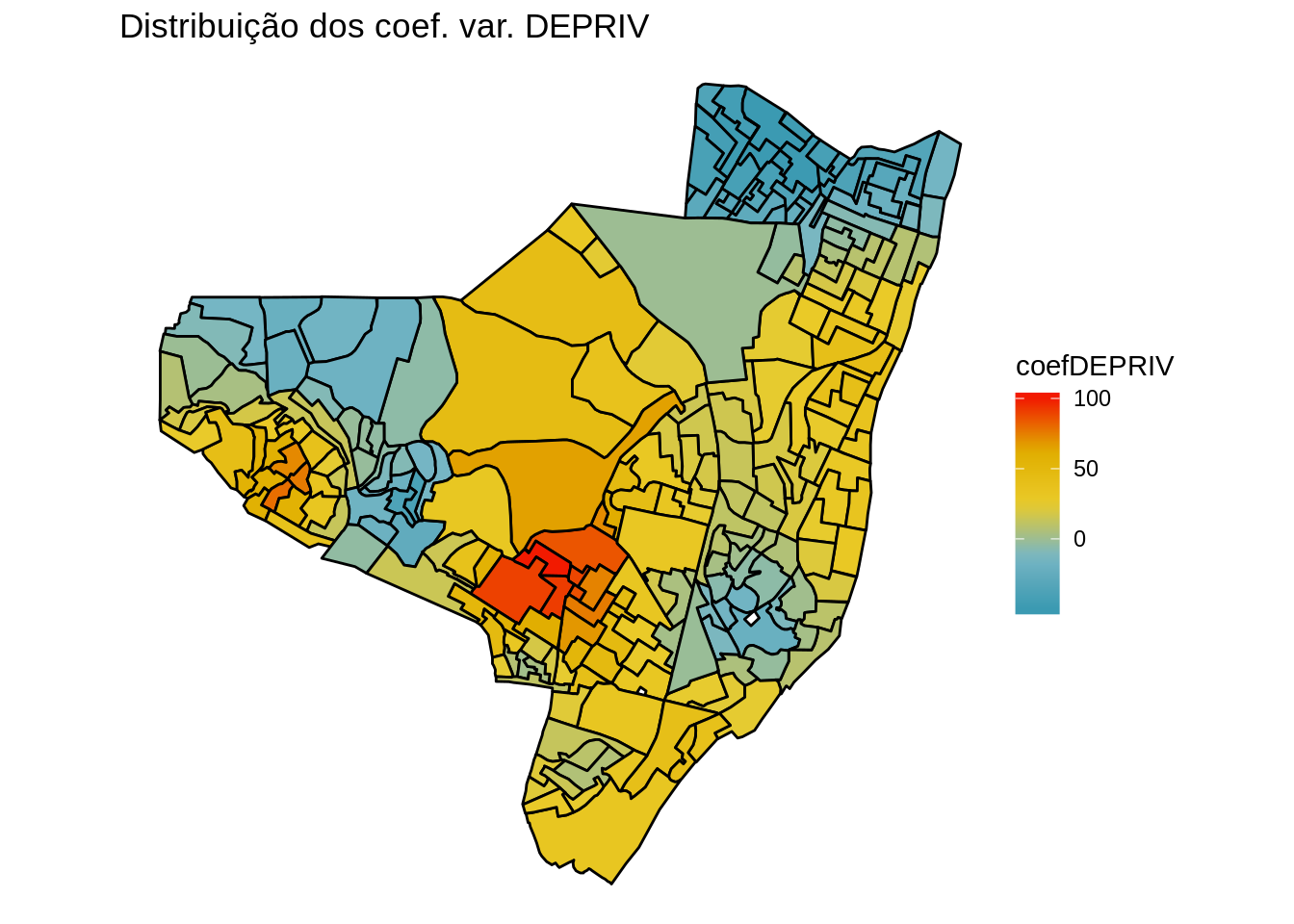
Mapa dos coeficientes de determinação regionalizados (\(R^2\) local).

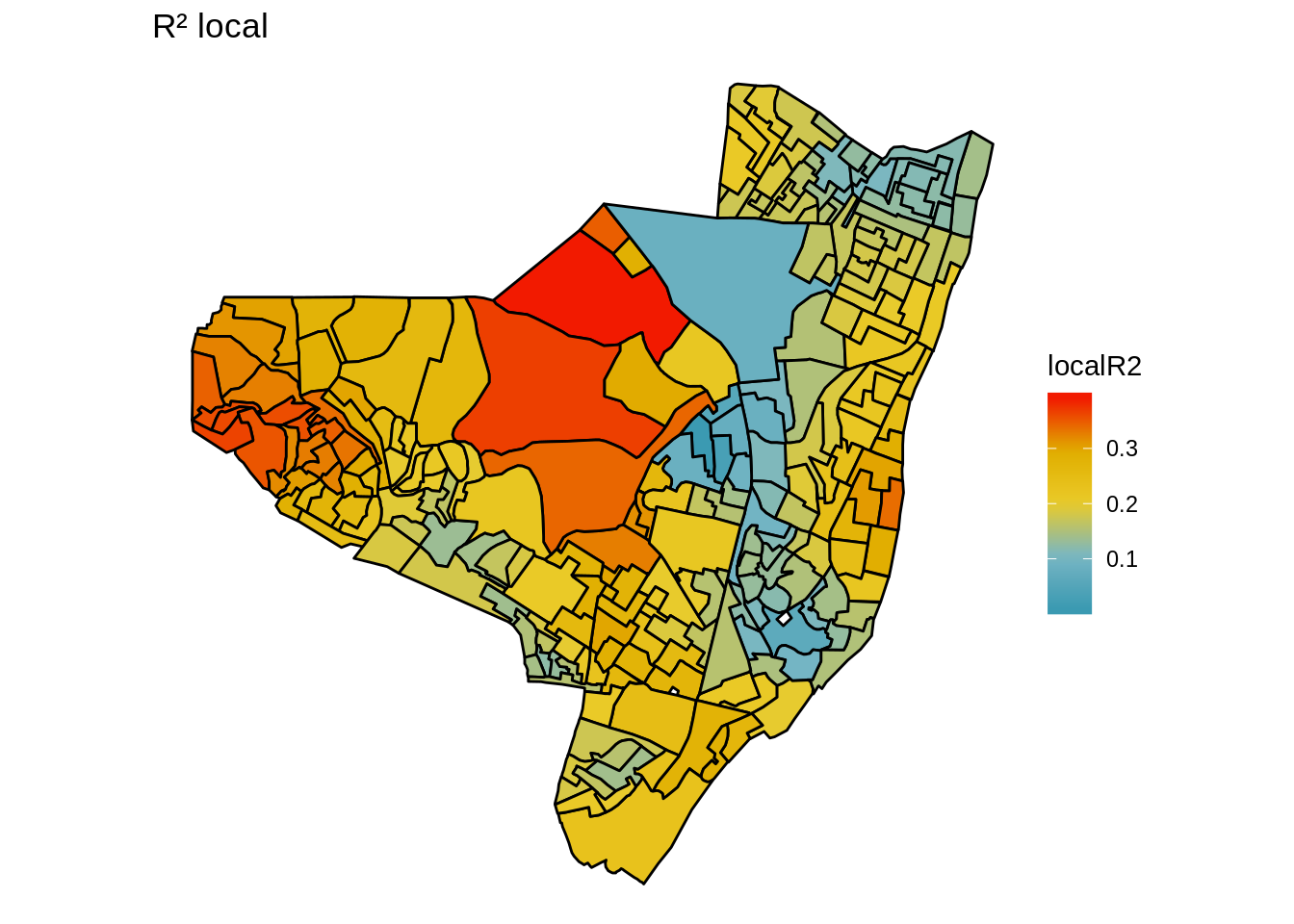
Mapa dos valores preditos a partir do GWR.

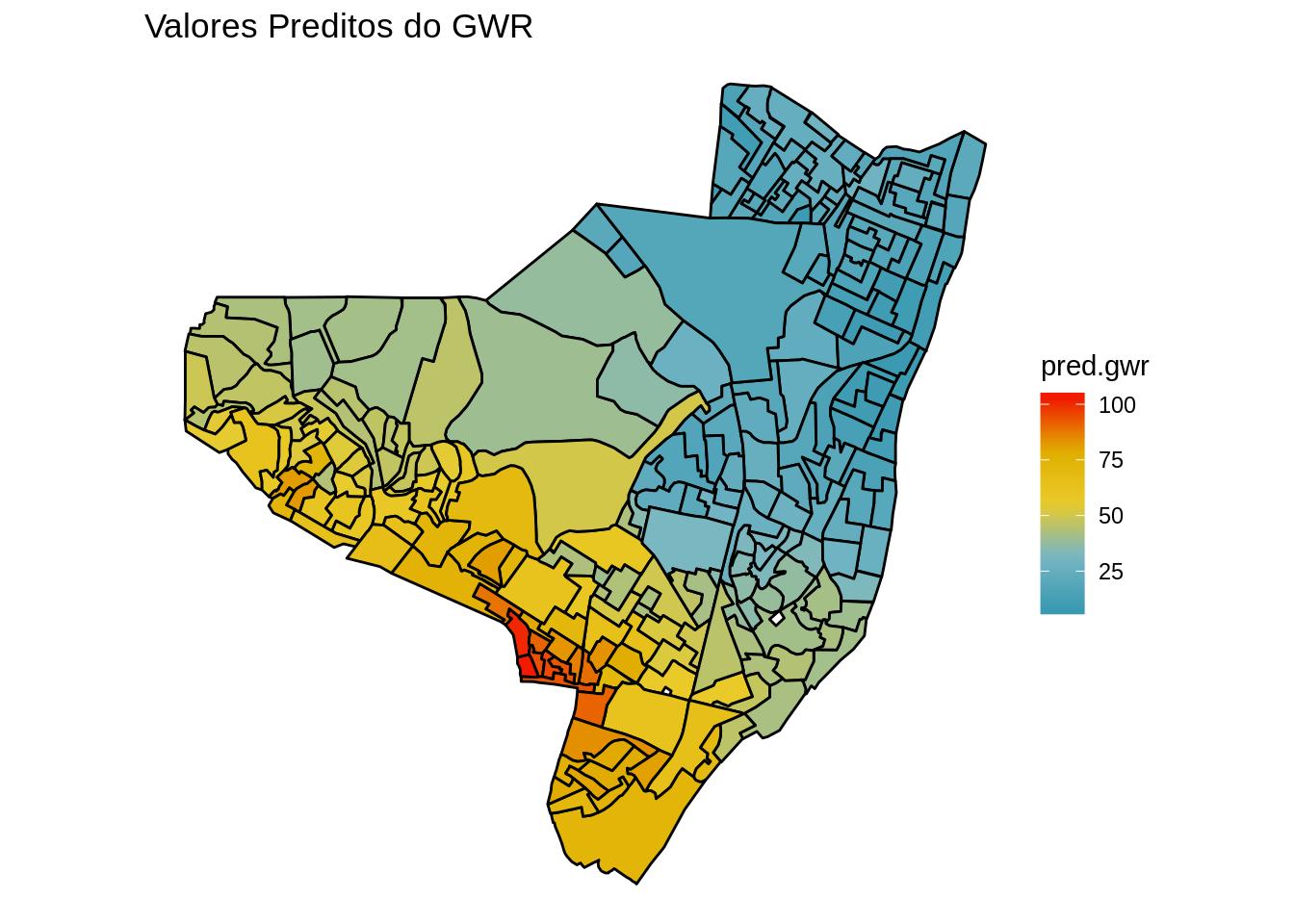
Vewrificando o processo de predição do modelo.

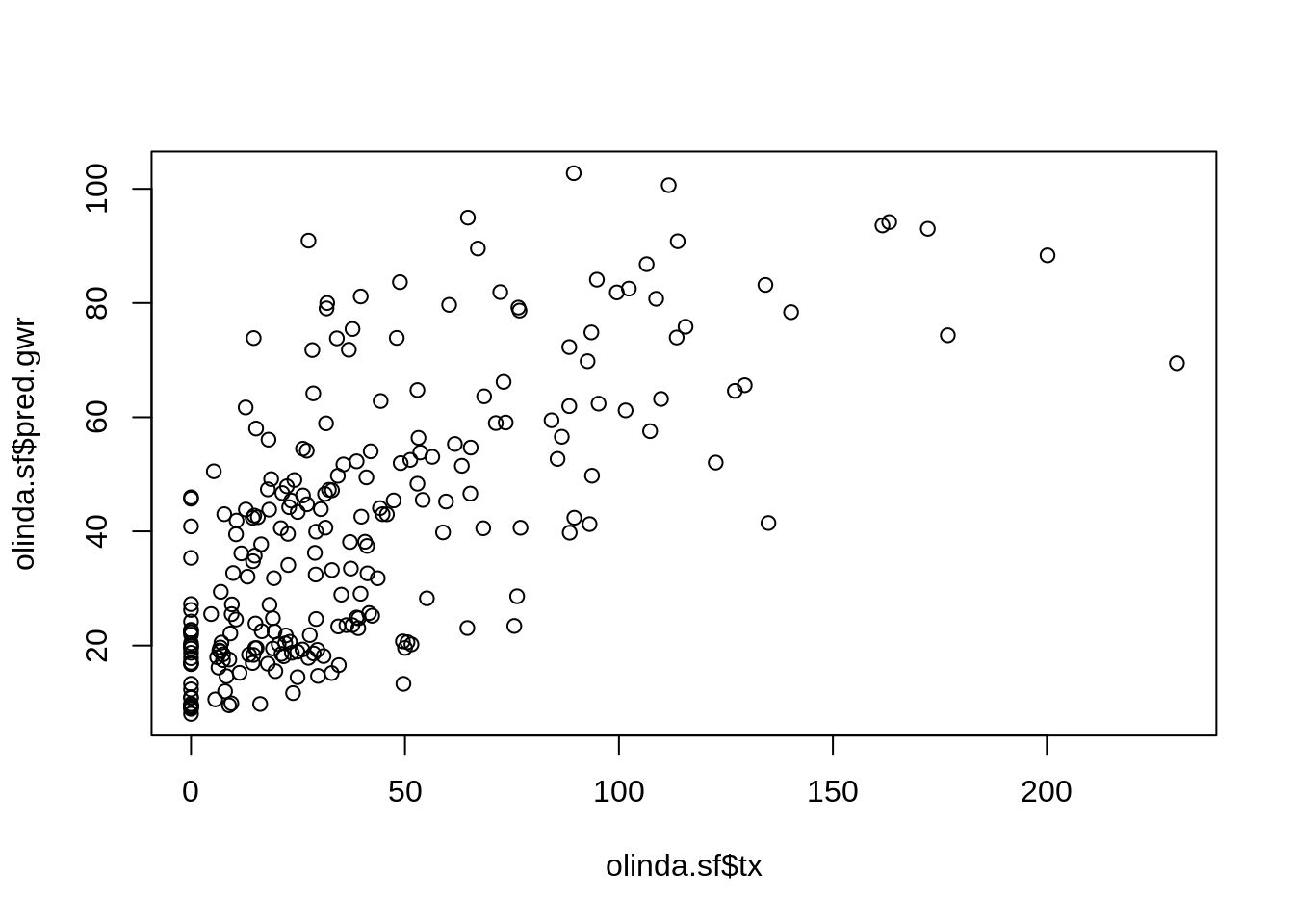
[1] 0.681

Verificando a autocorrelação espacial dos resíduos.


    Moran I test under randomisation

data:  (olinda.sf$tx - olinda.sf$pred.gwr)  
weights: pesos.viz    

Moran I statistic standard deviate = -0.78, p-value = 0.8
alternative hypothesis: greater
sample estimates:
Moran I statistic       Expectation          Variance 
        -0.034834         -0.004167          0.001545

Podemos verificar que a hipótese de autocorrelaçãofoi descartada.

10.8 ERRATA

O pacote spdep vai mudar e a partir da próxima versão não vais mais disponibilizar as funções de modelagem para SAR e CAR . O pacote spatialreg (Spatial Regression Analysis) devera ser usado. A função ** spautolm()** deve ser usada tanto para SAR quanto para o CAR usando a especificação family=“CAR” , family=“SAR” ou ainda family=“MA” este ultimo para modelos de médias moveis espaciais.

10.9 Bibliografia sugerida

Applied Spatial Data Analysis with R; Roger S. Bivand, Edzer Pebesma , Virgilio Gomez-Rubio Springer; Edição: 2nd ed. 2013

Fotheringham, A. S., Brunsdon, C., and Charlton, M. E. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships. Wiley, Chichester. 2002.

Lloyd, C. D. (2007). Local Models for Spatial Analysis. CRC, Boca Raton. Schabenberger, O. and Gotway, C. A. Statistical Methods for Spatial Data Analysis. Chapman & Hall, London. 2005.

Ver Hoef, Jay M.; Hanks, Ephraim M.; Hooten, Mevin B. On the relationship between conditional (CAR) and simultaneous (SAR) autoregressive models. Spatial statistics, v. 25, p. 68-85, 2018.

Waller, L. A. and Gotway, C. A. Applied Spatial Statistics for Public Health Data. Wiley, Hoboken, NJ. 2004.

Ward, M.D. and K.S. Gleditsch. Spatial Regression Models. Thousand Oaks, CA: Sage. 2008.

Wheeler, D. and Tiefelsdorf, M. Multicollinearity and correlation among local regression coefficients in geographically weighted regression. Journal of Geograph- ical Systems, 7:161–187. 2005.

  • Online

Geographically Weighted Regression - Roger Bivand (2017)

Coordinate Reference Systems(CRS)