11 Dados de Área III
11.1 Exemplo com os dados de dengue em Dourados/MS
Nesta aula serão utilizados os dados da monografia de Isis Rodrigues Reitman, apresentada ao Curso de Geografia da Faculdade de Ciências Humanas da Universidade Federal da Grande Douradosos/MS, em março de 2013. O título da monografia é “DISTRIBUIÇÃO ESPACIAL DOS CASOS DE DENGUE NO PERÍMETRO URBANO DE DOURADOS-MS E SUA RELAÇÃO COM OS FATORES SOCIOAMBIENTAIS E POLÍTICOS”
ATENÇÃO ATENÇÃO ATENÇÃO
Devido a maneira que o Windows acessa as url usando a internet é necessario mudar a opção default dele para que possa usar apropiadamenet os recursos https, ftps, etc… A linha abaixo deve ser utilizanda antes de usar as funções que acessam esse tipo de recurso.
Lendo a tabela da população por setor censitário e baixando os shapes files do contorno e por setor censitário de Dourados/MS
local <- 'https://gitlab.procc.fiocruz.br/oswaldo/eco2019/raw/master/dados/'
pop2010 <- read_csv(paste0(local,'pop2010.csv'))
tmpdir <- tempdir()
download.file(paste0(local,'setores_dourados.zip'),
destfile = paste0(tmpdir,'/dourados.zip'))
unzip(zipfile = paste0(tmpdir,'/dourados.zip'),exdir = tmpdir)
dir(tmpdir) [1] "contorno.dbf" "contorno.sbn" "contorno.sbx" "contorno.shp" "contorno.shx" "dourados.zip" "file23567ef49e7a" "olinda.dbf" "olinda.shp" "olinda.shx" "olinda.zip" "Setor_UTM_SIRGAS.dbf" "Setor_UTM_SIRGAS.prj" "Setor_UTM_SIRGAS.sbn" "Setor_UTM_SIRGAS.sbx" "Setor_UTM_SIRGAS.shp" "Setor_UTM_SIRGAS.shx"setor.sf <- read_sf(paste0(tmpdir,'/Setor_UTM_SIRGAS.shp'), crs = 31981)
contorno.sf <- read_sf(paste0(tmpdir,'/contorno.shp'), crs = 31981)Fazendo um join com as tabelas com os setores censitários + popoulação
[1] "contorno.dbf" "contorno.sbn"
[3] "contorno.sbx" "contorno.shp"
[5] "contorno.shx" "dourados.zip"
[7] "Setor_UTM_SIRGAS.dbf" "Setor_UTM_SIRGAS.prj"
[9] "Setor_UTM_SIRGAS.sbn" "Setor_UTM_SIRGAS.sbx"
[11] "Setor_UTM_SIRGAS.shp" "Setor_UTM_SIRGAS.shx" - Lendo e plotando os casos de dengue georreferenciados em Dourados/MS
casos <- read_csv(paste0(local,'dengue_dourados.csv'))
casos.sf <- st_as_sf(casos, coords = c("X", "Y"), crs = 31981)
ggplot(setor.sf) +
geom_sf(fill = 'white', color='black') +
geom_sf(data=casos.sf, color='red',size=1) +
theme_void()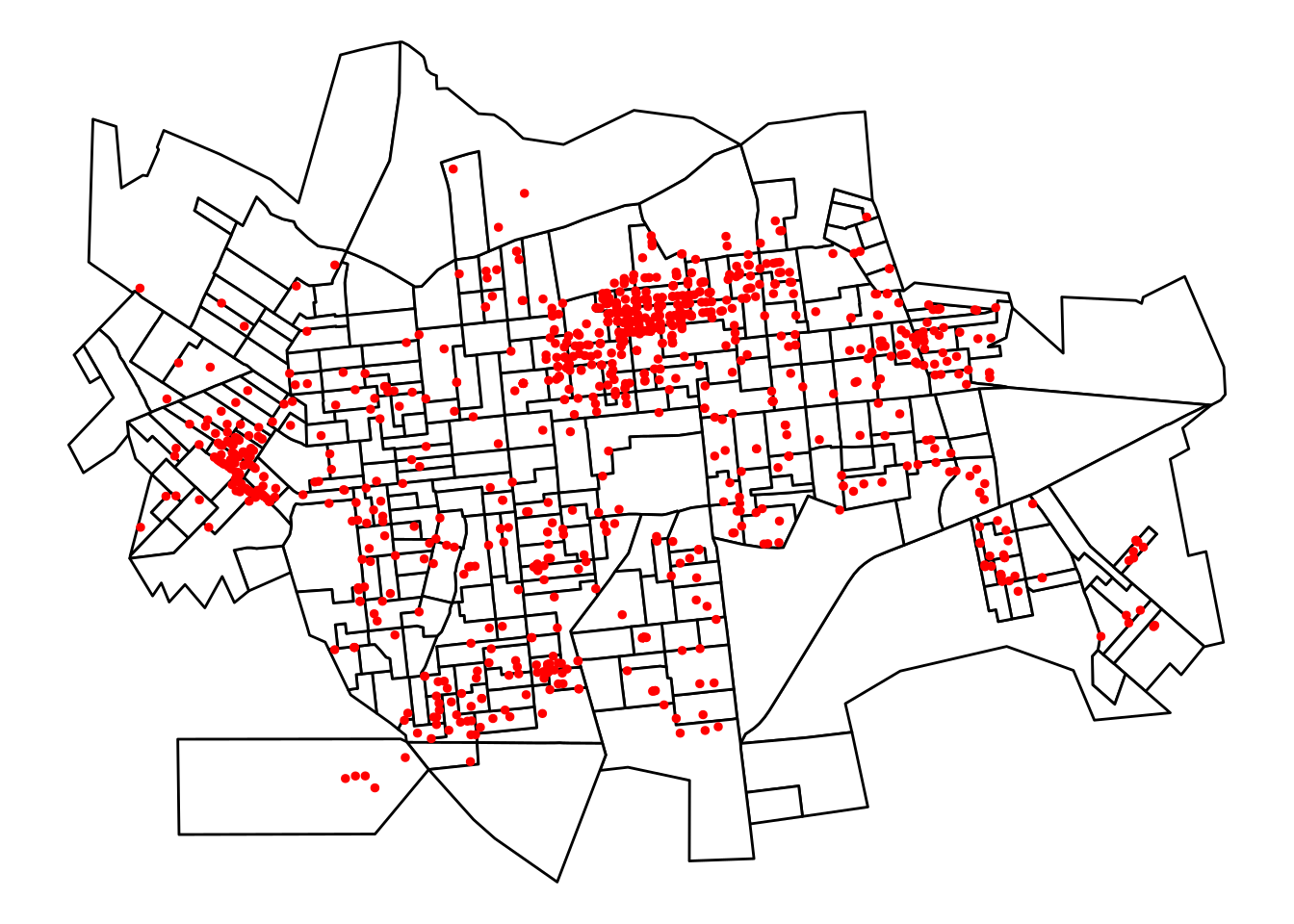
- Lendo e plotando os os pontos de coleta de lixo georreferenciados em Dourados/MS
lixo <- read_csv2('~/Documentos/cursos_ecologicos_2019/Bookdown/dados/lixo_dourados.csv')
lixo.sf <- st_as_sf(lixo, coords = c("X", "Y"), crs = 31981)
ggplot(setor.sf) +
geom_sf(fill = 'white', color = 'black') +
geom_sf(data=lixo.sf,color='blue',size=1) +
theme_void()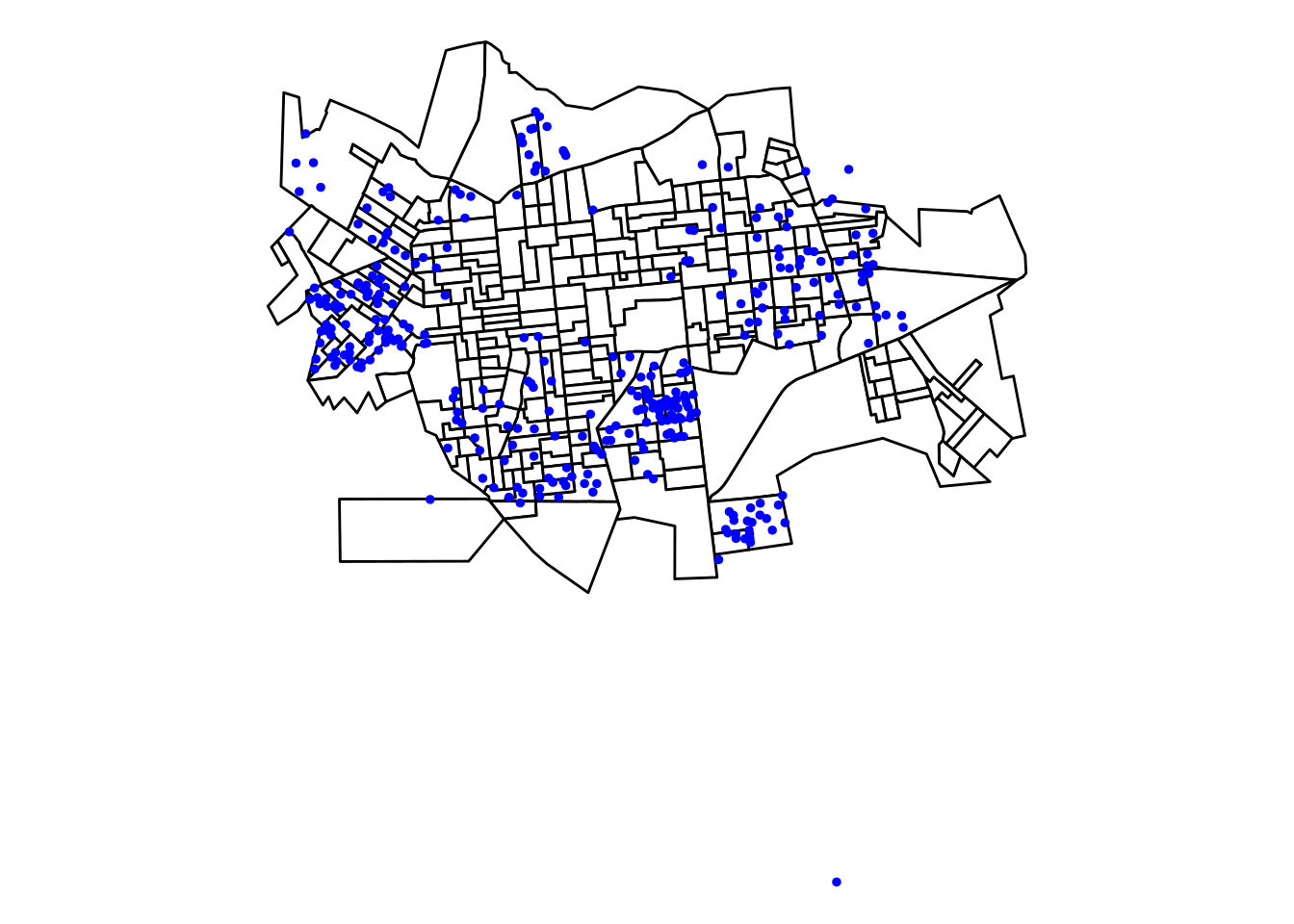
Como podemos observar, existem alguns pontos de coleta de lixo fora do contorno de Dourados/MS. Uma forma de ficarmos só com os pontos dentro do polígono é utilizando o comando st_intersection.
lixo2.sf <- st_intersection(contorno.sf, lixo.sf)
# ou lixo2.sf <- st_intersection(setor.sf, lixo.sf)
ggplot(setor.sf) +
geom_sf(fill = 'white', color = 'black') +
geom_sf(data=lixo2.sf,color='blue',size=1) +
theme_void()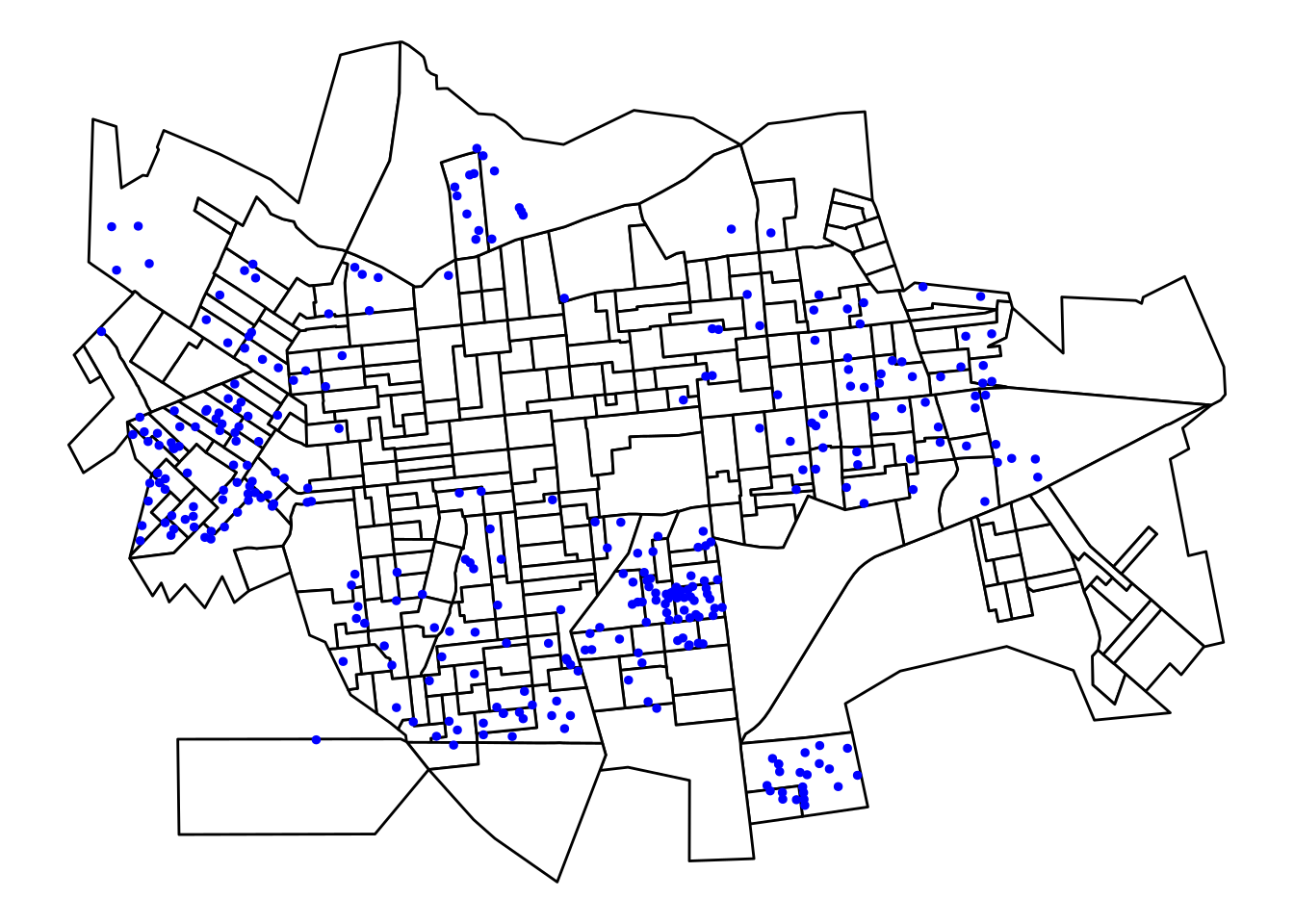
Verificando as paletas de cores.

Utilizando as informações dos casos (pontos) + do lixo (ponto) + população de cada setor censitário (mapa temático)
ggplot(setor.sf) +
geom_sf(aes(fill=pop)) +
geom_sf(data=casos.sf,color='red',size=0.7, aes(colour = "Caso"),
show.legend = "point") +
geom_sf(data=lixo2.sf,color='salmon',size=1, aes(colour = "Lixo"),
show.legend = "point") +
scale_fill_distiller(palette ="PuBu", direction = 1) +
scale_colour_manual(values = c("Caso" = "red", "Lixo" = "slamon")) +
theme_minimal()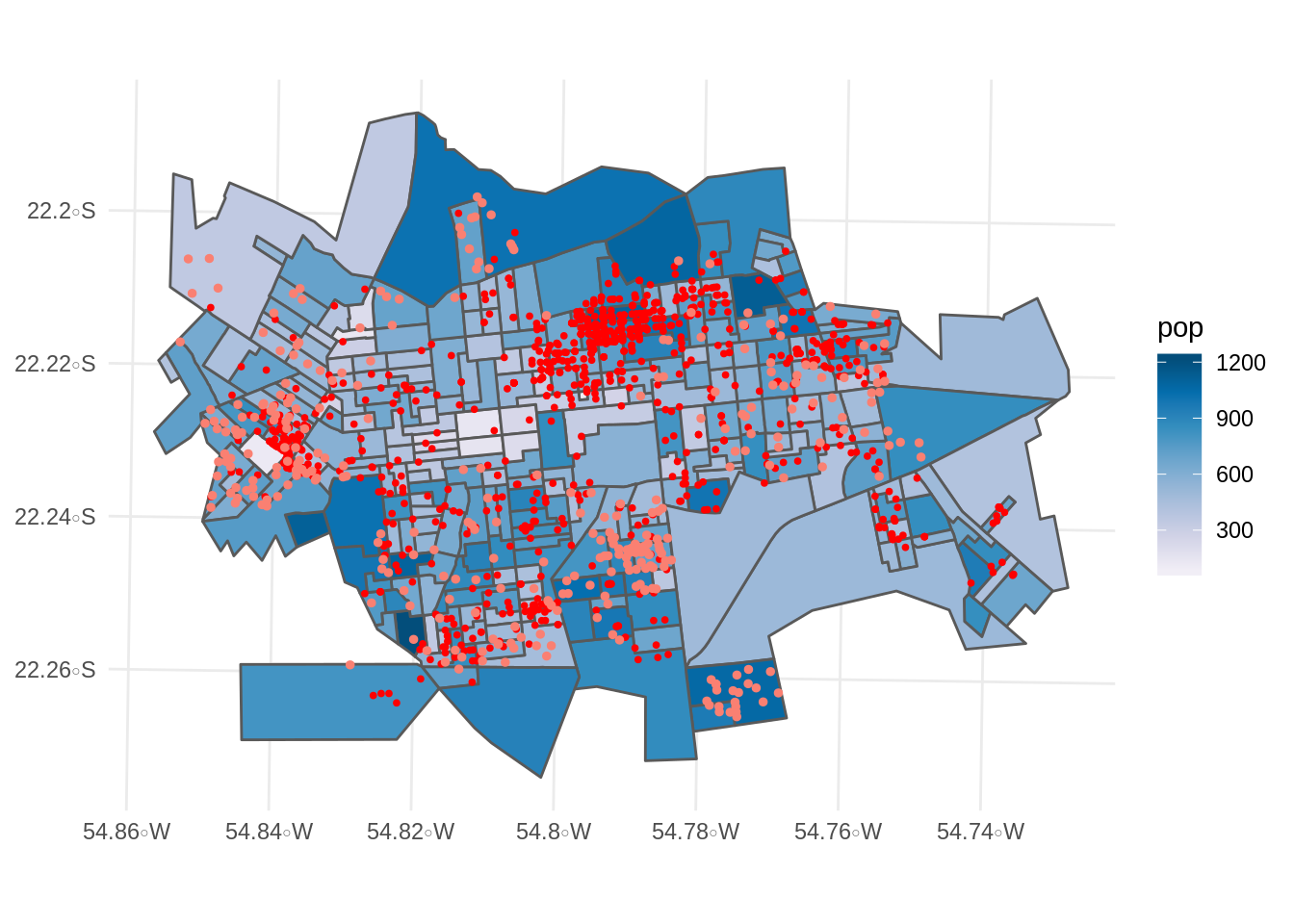
Iremos agora construir buffers de 500m de distância ao redor de cada ponto de coleta de lixo. Isso é interessante para verificar se os casos de dengue ocorrem em um raio de até 500m de distância dos pontos de coleta de lixo. Ou seja, a pergunta é, será que a distância dos pontos de coeta de lixo influenciam a ocorrência do caso de dengue ?
Buffers: São polígonos que contornam um objeto a uma determinada distância. Sua principal função é materializar os conceitos de “perto” e “longe”.
lixo_buffer <- st_buffer(lixo2.sf, 500)
ggplot(setor.sf) +
geom_sf(aes(fill=pop)) +
geom_sf(data=lixo_buffer,color='gray', fill = "transparent", size=0.4) +
geom_sf(data=casos.sf, color='red',size=0.7) +
scale_fill_distiller(palette ="PuBu", direction = 1) +
scale_colour_manual(values = c("Caso" = "red", "Lixo" = "slamon")) +
theme_minimal()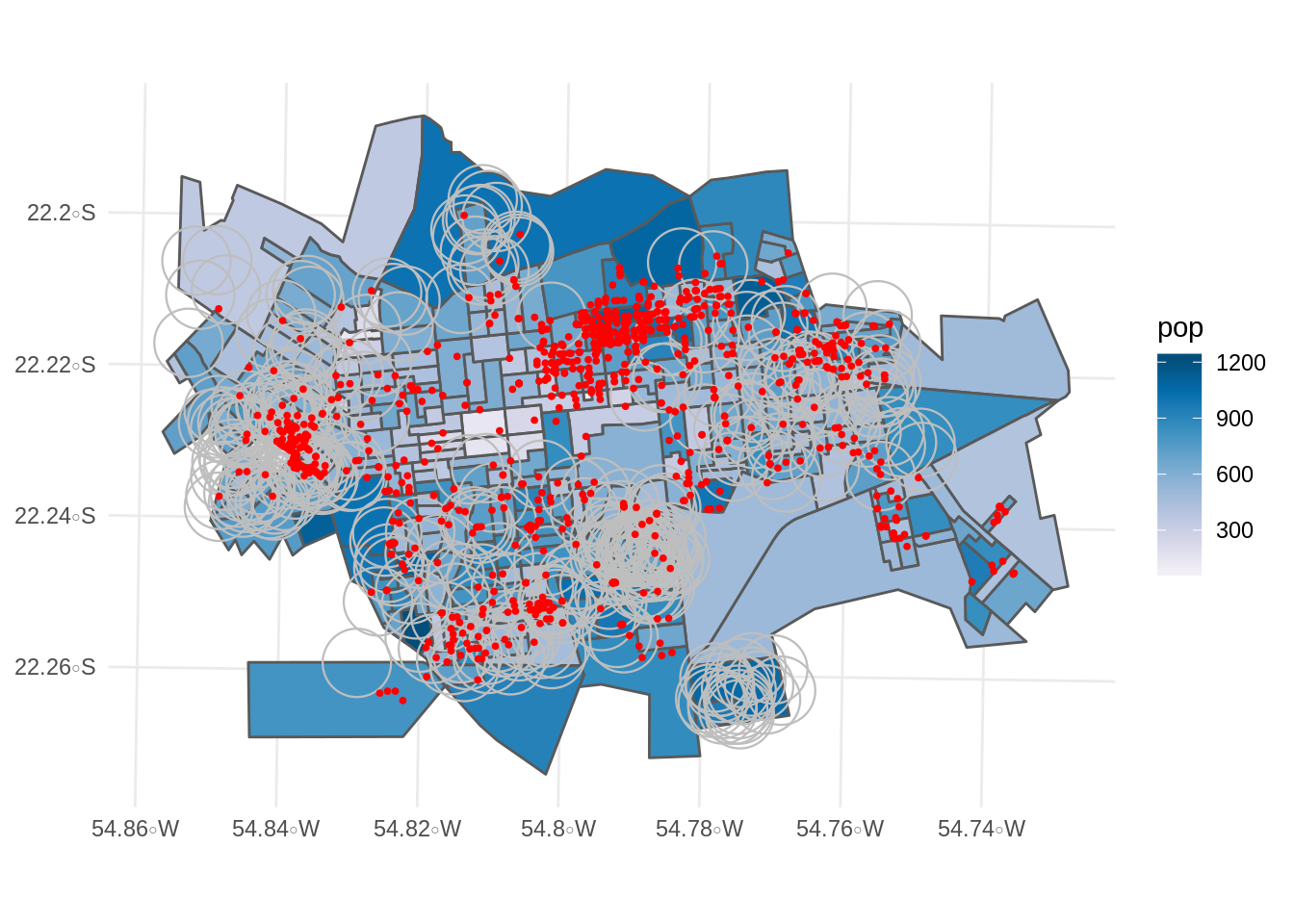
Represntando os casos e o lixo de forma interativa.
tm_shape(setor.sf) + tm_borders("black") +
tm_shape(casos.sf) + tm_dots("red") +
tm_shape(lixo.sf) + tm_dots("green") +
tm_shape(lixo_buffer) + tm_borders("blue") +
tmap_mode("view")## conta casos por setor
casos.sf$contador <- 1
casos <- setor.sf %>%
st_join(casos.sf) %>%
filter(CLASSI_FIN == 1) %>% ## seleciona somente os casos confirmados
group_by(ID) %>%
summarise(casos = sum(contador))
st_geometry(casos) <- NULL ## remove atributos de geometria
## numero de depositos de Lixo por setor
lixo.sf$contador <- 1
lixo <- setor.sf %>%
st_join(lixo.sf) %>%
group_by(ID) %>%
summarise(lixo = sum(contador))
st_geometry(lixo) <- NULL ## remove atributos de geometria
# Inserindo as contagens dos casos e de pontos de coleta de lixo no atributo com a geometria.
setor.sf <- setor.sf %>%
left_join(lixo,by = 'ID') %>%
left_join(casos,by = 'ID') Plotando o mapa temático dos casos por setor censitário
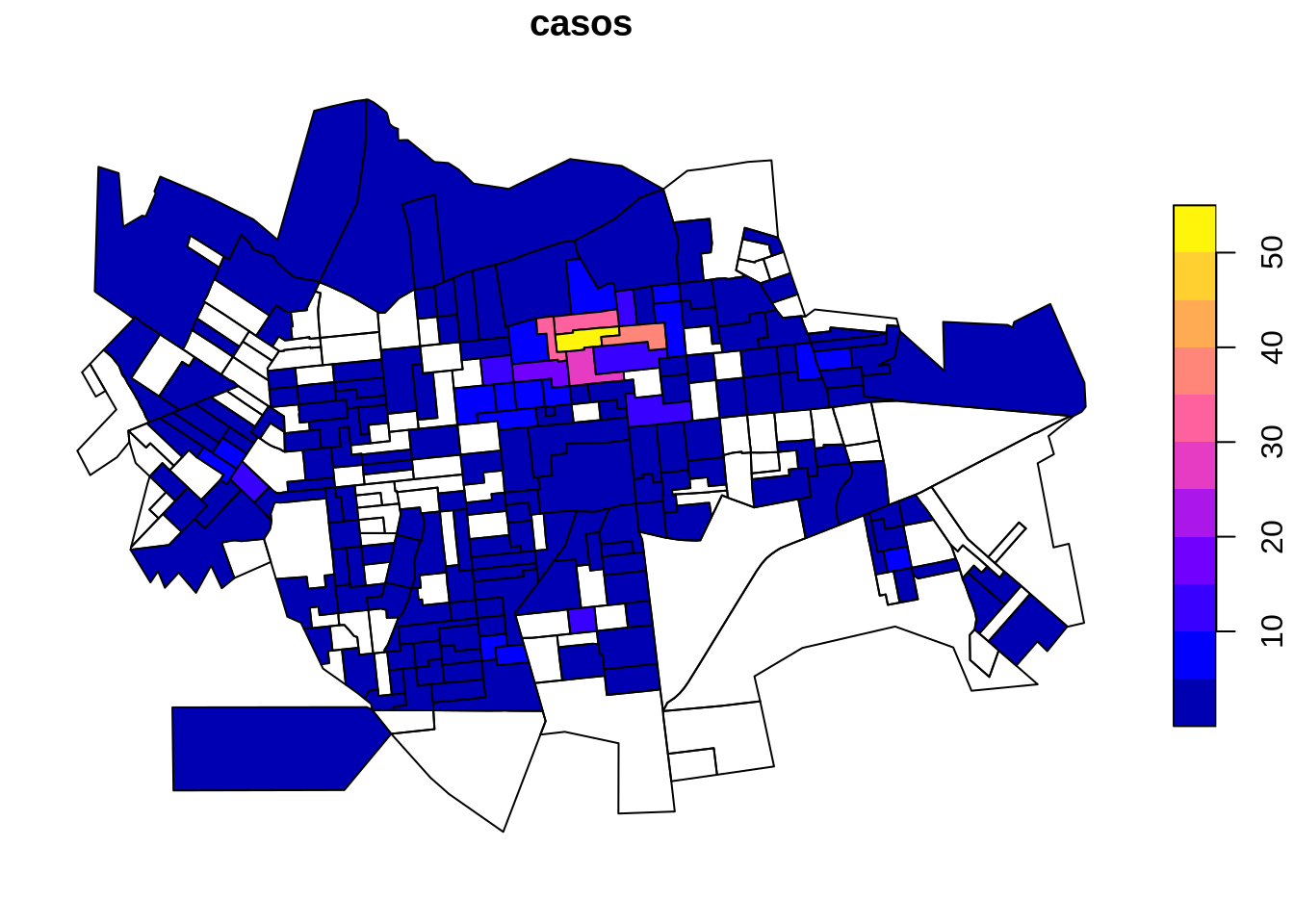
Plotando o mapa temático dos pontos de coleta de lixo por setor censitário
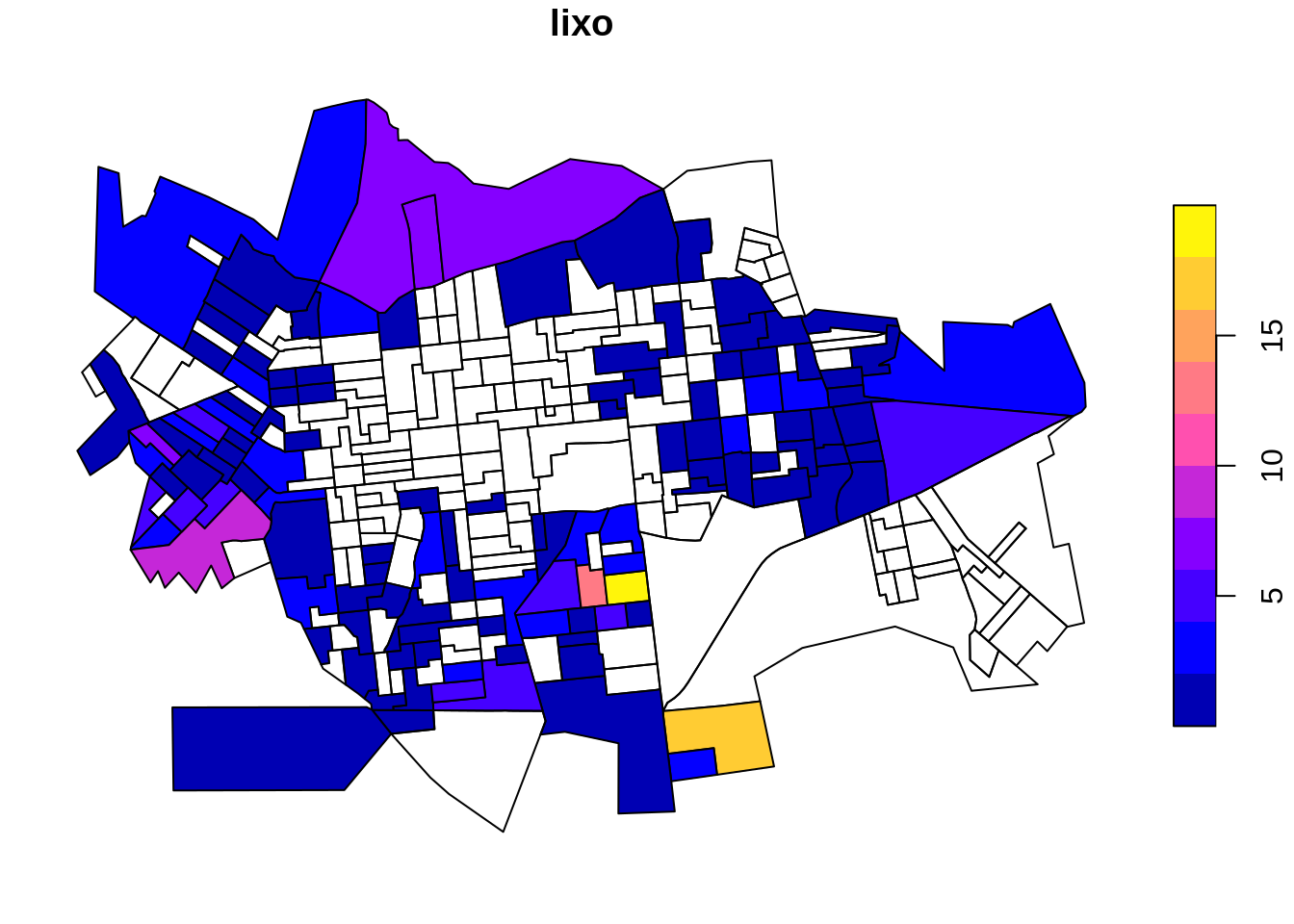
Calculando a taxa de incidência e plotando o mapa temático dos pontos de coleta de lixo por setor censitário
setor.sf$tx <- (setor.sf$casos/setor.sf$pop) * 1000
setor.sf$tx[is.na(setor.sf$tx)] <- 0 # Transformando os missings em zero
summary(setor.sf$tx) Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00 0.00 1.74 4.06 4.31 56.40 library(wesanderson)
pal <- wes_palette("Moonrise3", 20, type = "continuous")
ggplot(setor.sf) +
geom_sf(aes(fill = tx), color = 'black') +
scale_fill_gradientn(colours = pal) +
ggtitle("Taxa de incidência de Dengue") +
theme_void()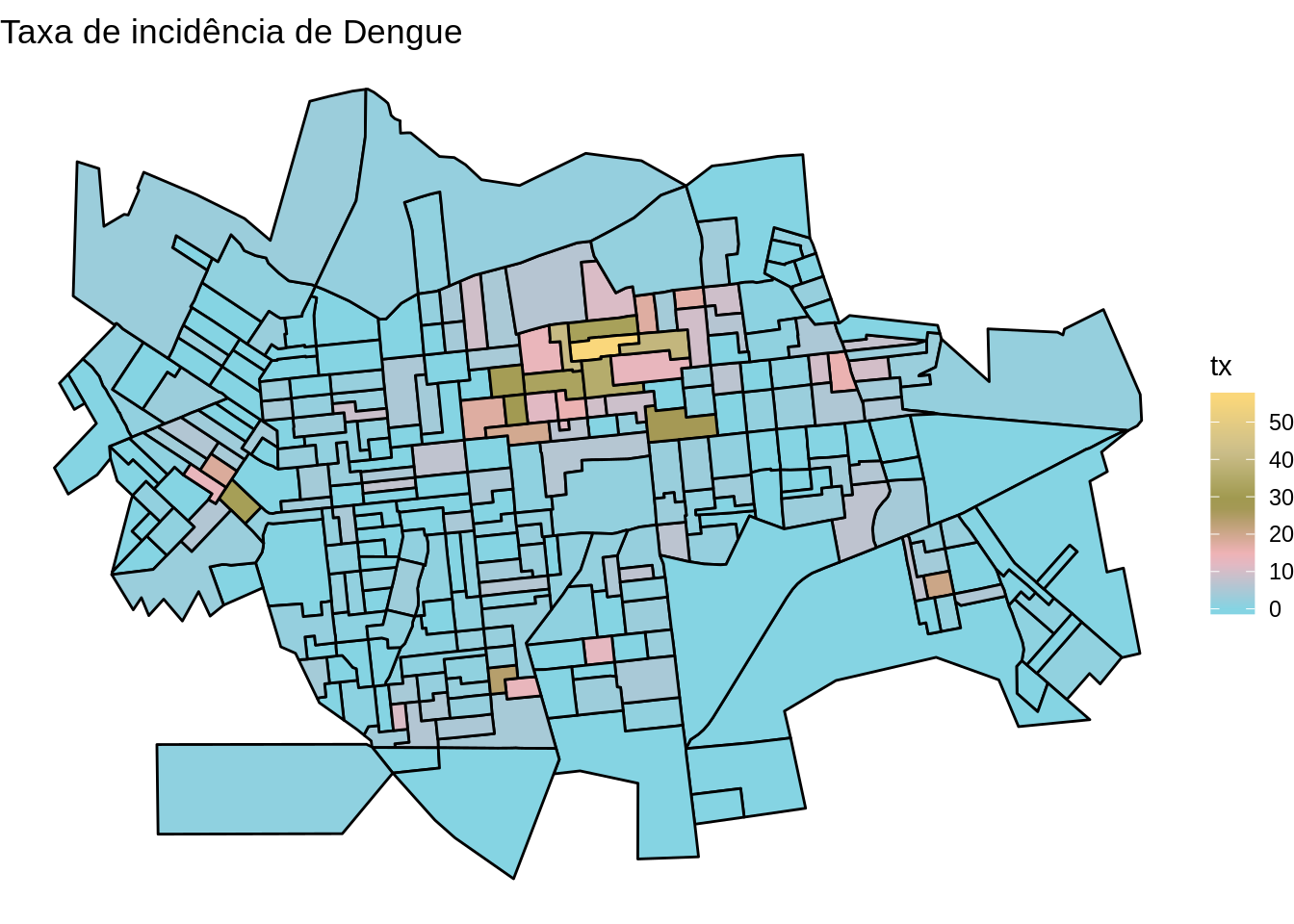
11.2 Kernel por atributos
Vamos plotar o kernel por atributos referente a taxa de incidência de dengue em Dourados/MS.
Primeiramente é necessário dissolver os poligonos em formato sf para obter o contorno. Nesse caso queremos preservar o atributo AREA
Extraindo os centróidas dos polígonos em Dourados/MS.
centroides <- st_centroid(st_geometry(setor.sf))
# Transformando em os centróides em formato sp
centroides.sp <- as.data.frame(as_Spatial(centroides))
names(centroides.sp) <- c('X','Y')
plot(centroides.sp)
Colocando os pontos no formato sp
centroides.ppp <- ppp(centroides.sp$X,centroides.sp$Y, dourados.w)
plot(centroides.ppp,pch=19,cex=0.5)
Fazendo o kernel por atributo da taxa de detecção
kernel.tx <- density(centroides.ppp, 500, weights = setor.sf$tx, scalekernel = TRUE)
plot(kernel.tx)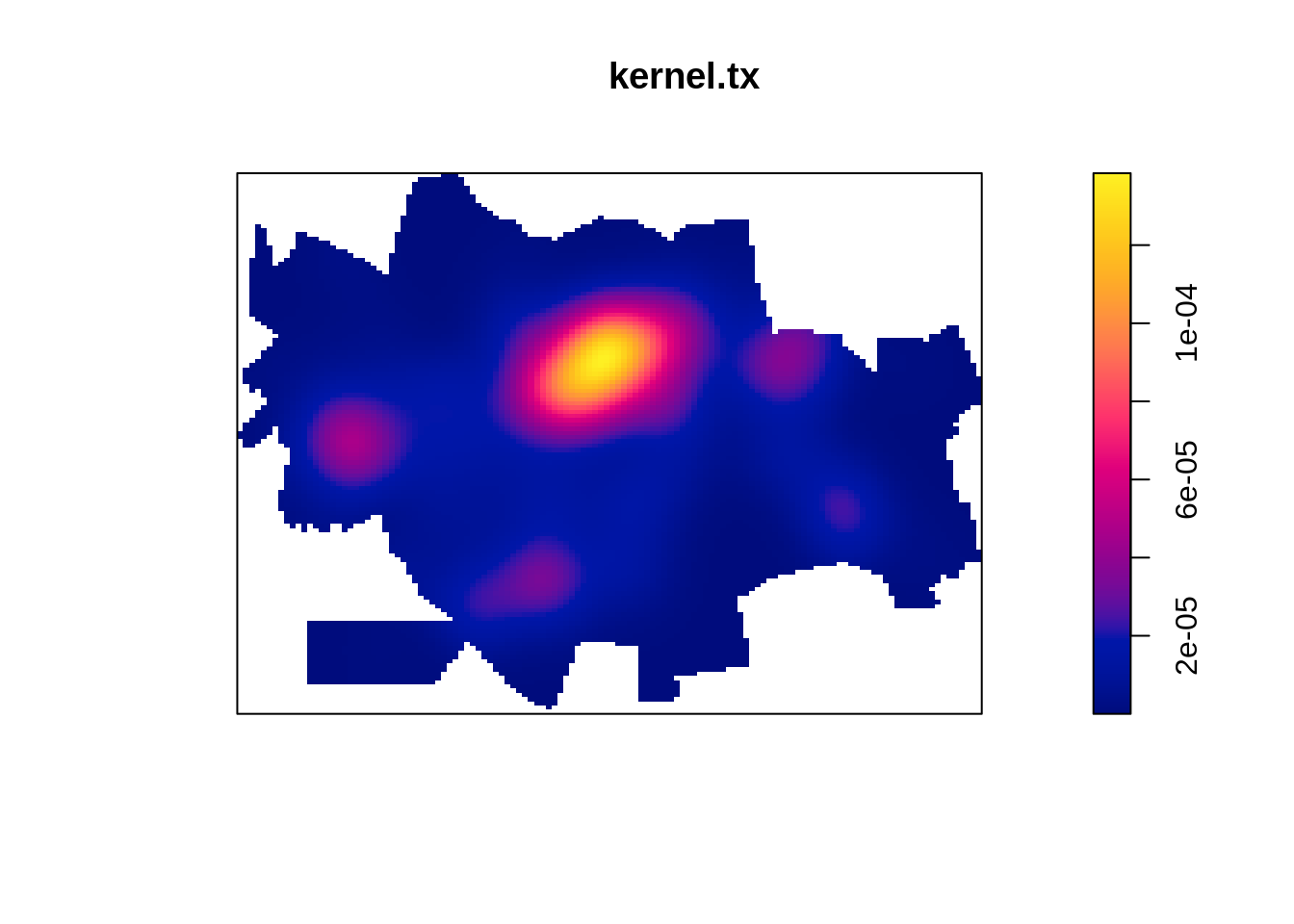
Construindo a matriz de vizinhança para verificar a autocorrelação espacial.
Neighbour list object:
Number of regions: 284
Number of nonzero links: 1726
Percentage nonzero weights: 2.14
Average number of links: 6.077 Iremos precisar da coordenadas dos centróides
setor.sp <- as(setor.sf, 'Spatial') # convertendo em formato sp
coord <- coordinates(setor.sp) # coordenadas dos centroidas dos poligonos de dourados
class(setor.sp)[1] "SpatialPolygonsDataFrame"
attr(,"package")
[1] "sp"11.3 Matriz de Vizinhança
Iremos precisar da coordenadas dos centróides
setor.sp <- as(setor.sf, 'Spatial') # convertendo em formato sp
coord <- coordinates(setor.sp) # coordenadas dos centroidas dos poligonos de dourados
class(setor.sp)[1] "SpatialPolygonsDataFrame"
attr(,"package")
[1] "sp"11.4 Matriz de Vizinhança
Verificando a malha de conectividade da vizinhança de Dourados/MS
viz.sf <- as(nb2lines(viz, coords = coord), 'sf')
viz.sf <- st_set_crs(viz.sf, st_crs(setor.sf))
# Plota o grafo de conectividade por contiguidade
mapa.viz <- ggplot(setor.sf) +
geom_sf(fill = 'salmon', color = 'white') +
geom_sf(data = viz.sf) +
theme_minimal() +
ggtitle("Vizinhança por \n conectividade") +
ylab("Latitude") +
xlab("Longitude")
mapa.viz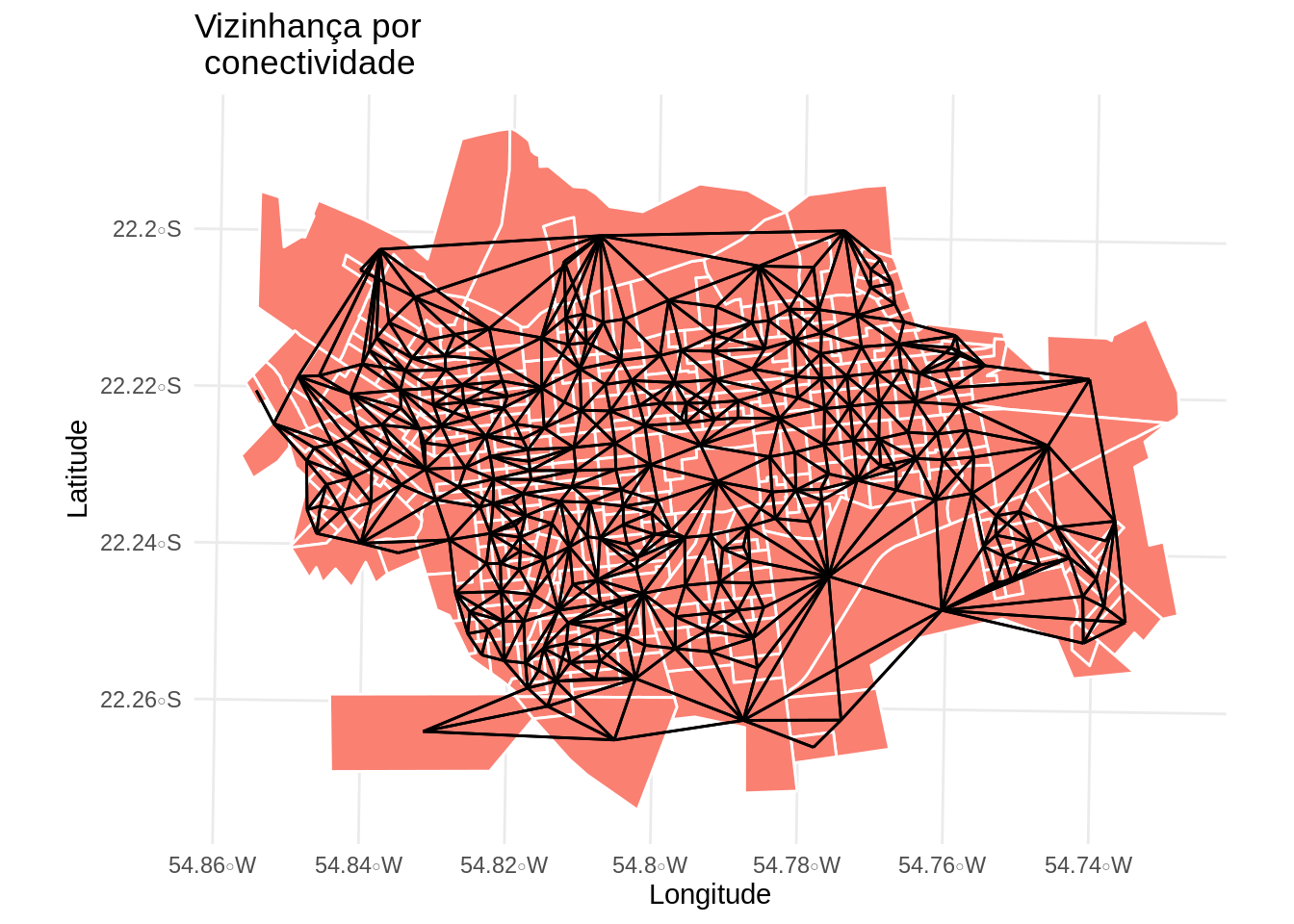
11.5 Autocorrelação Espacial
Obtendo a correlação da taxa de incidência de dengue Dourados/MS
Moran I test under randomisation
data: setor.sf$tx
weights: pesos.viz
Moran I statistic standard deviate = 16, p-value <2e-16
alternative hypothesis: greater
sample estimates:
Moran I statistic Expectation Variance
0.524720 -0.003534 0.001129 Plotando o correlograma
Spatial correlogram for setor.sf$tx
method: Moran's I
estimate expectation variance standard deviate Pr(I) two sided
1 (284) 0.524720 -0.003534 0.001129 15.72 < 2e-16 ***
2 (284) 0.237768 -0.003534 0.000485 10.95 < 2e-16 ***
3 (284) 0.095366 -0.003534 0.000284 5.87 4.3e-09 ***
4 (284) -0.020634 -0.003534 0.000197 -1.22 0.224
5 (284) -0.075892 -0.003534 0.000167 -5.59 2.2e-08 ***
6 (284) -0.064484 -0.003534 0.000162 -4.79 1.6e-06 ***
7 (284) -0.027083 -0.003534 0.000167 -1.82 0.069 .
8 (284) -0.027445 -0.003534 0.000183 -1.77 0.077 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1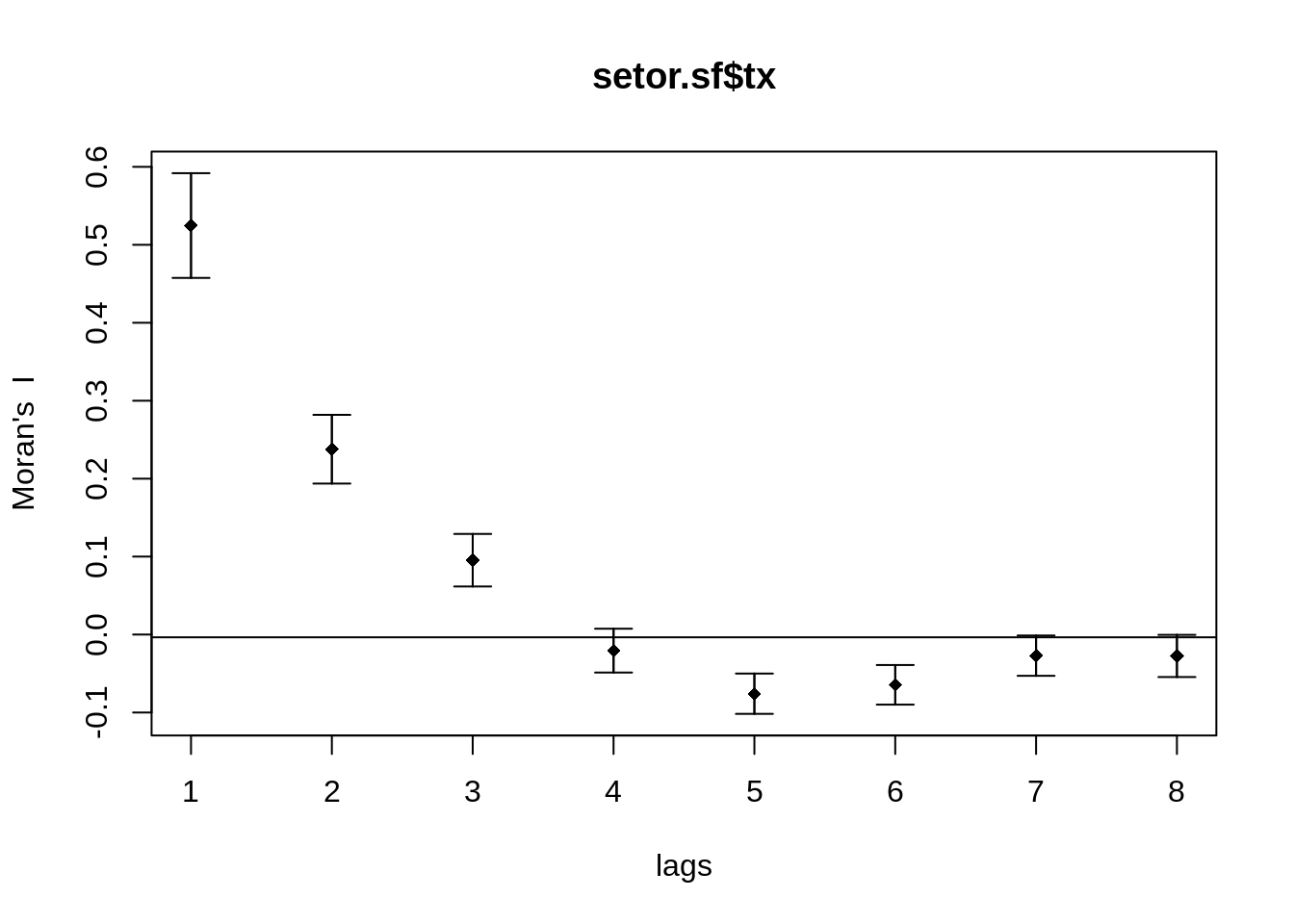
Mapeando os polígonos que tiveram os p-valores mais significativos no Moran Local.
setor.sf$pval <- localmoran(setor.sf$tx, pesos.viz)[,5]
tm_shape(setor.sf) +
tm_polygons(col='pval', title="p-valores", breaks=c(0, 0.01, 0.05, 0.10, 1), border.col = "white", palette="-Oranges") +
tm_scale_bar(width = 0.15) Moran Local (Lisa Map) da taxa de incidência Dourados/MS
Local Morans I Stand. dev. (N) Pr. (N) Saddlepoint Pr. (Sad) Expectation Variance Skewness Kurtosis Minimum Maximum omega sad.r sad.u
1 1 -0.009885 -0.01575 0.50628 -0.03601 0.51436 -0.003534 0.1626 -0.05148 8.753 -57.75 56.75 -0.0001370 -0.01569 -0.01570
2 2 0.226981 0.46512 0.32092 0.70056 0.24179 -0.003534 0.2456 -0.04188 8.753 -70.87 69.87 0.0028119 0.44473 0.49832
3 3 -0.010911 -0.01830 0.50730 -0.04042 0.51612 -0.003534 0.1626 -0.05148 8.753 -57.75 56.75 -0.0001591 -0.01823 -0.01823
4 4 0.484676 1.31014 0.09507 1.43930 0.07503 -0.003534 0.1389 -0.05570 8.754 -53.41 52.41 0.0066304 1.08298 1.59298
5 5 0.018649 0.05953 0.47627 0.09384 0.46262 -0.003534 0.1389 -0.05570 8.754 -53.41 52.41 0.0005595 0.05930 0.05942
6 6 0.045043 0.13961 0.44448 0.22936 0.40930 -0.003534 0.1211 -0.05966 8.754 -49.91 48.91 0.0013876 0.13866 0.14041
7 7 0.107199 0.31825 0.37515 0.50632 0.30631 -0.003534 0.1211 -0.05966 8.754 -49.91 48.91 0.0029656 0.31095 0.33043
8 8 0.153965 0.42266 0.33627 0.64704 0.25880 -0.003534 0.1389 -0.05570 8.754 -53.41 52.41 0.0034865 0.40708 0.44885
9 9 -0.109294 -0.28382 0.61172 -0.46939 0.68060 -0.003534 0.1389 -0.05570 8.754 -53.41 52.41 -0.0024730 -0.27705 -0.29222
10 10 -0.147818 -0.32607 0.62781 -0.52794 0.70123 -0.003534 0.1958 -0.04691 8.753 -63.33 62.33 -0.0023467 -0.31667 -0.33858setor.sf$MoranLocal <- summary(resI)[,1]
library(scales)
ggplot(setor.sf) +
geom_sf(aes(fill = MoranLocal), color = 'black') +
scale_fill_gradientn(colours=c("blue", "white", "red"),
values=rescale(c(min(setor.sf$MoranLocal), 0, max(setor.sf$MoranLocal))), guide="colorbar") +
ggtitle("Moran local") +
theme_void()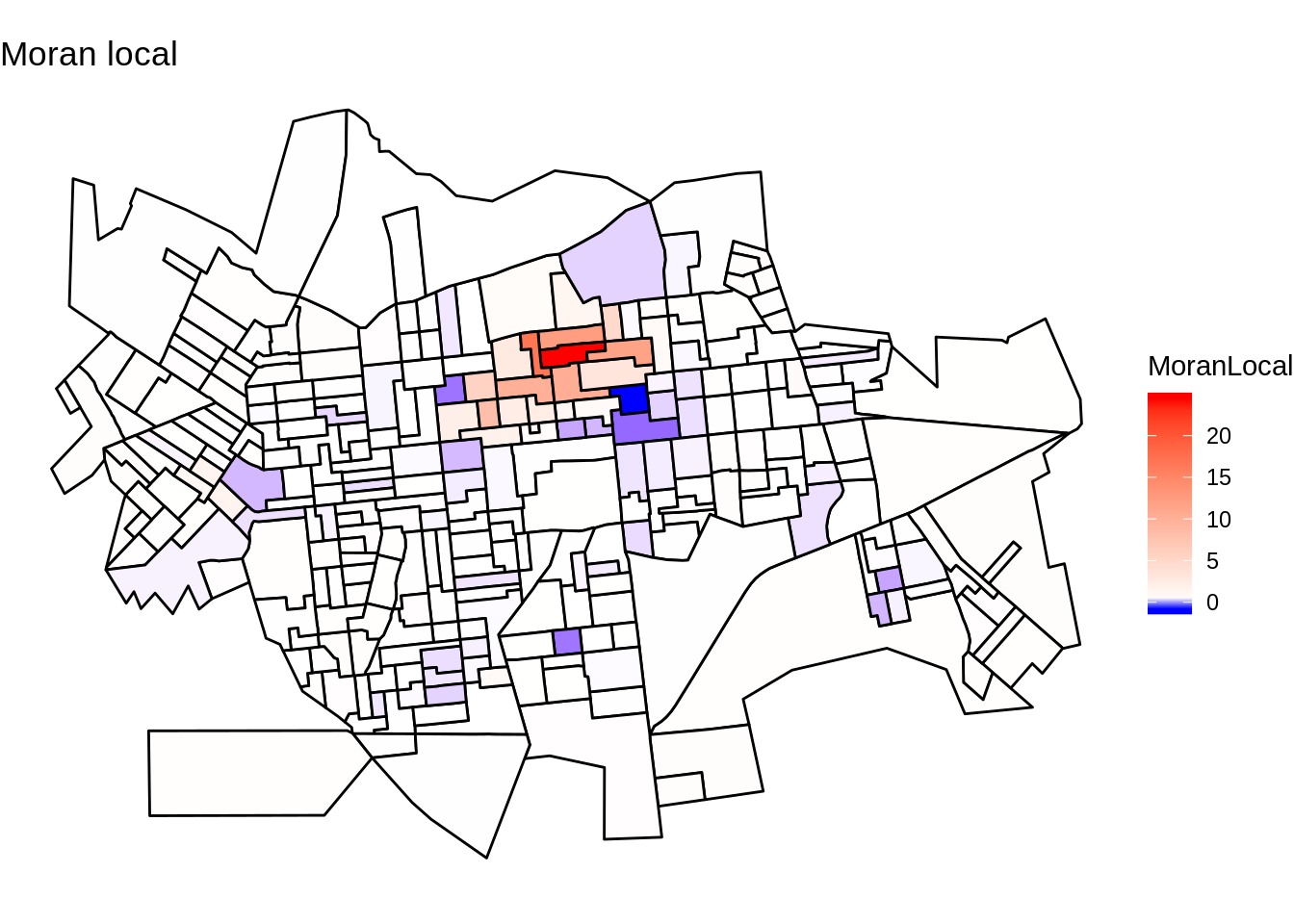
11.6 Modelos Linear, CAR e GWR
Ajustando o modelo de regressão linear simples.
setor.sf$lixo[is.na(setor.sf$lixo)] <- 0 # Transformando os missings em zero
dourados.lm <- lm(tx ~ lixo, data=setor.sf)
summary(dourados.lm)
Call:
lm(formula = tx ~ lixo, data = setor.sf)
Residuals:
Min 1Q Median 3Q Max
-4.51 -4.11 -2.29 0.24 51.89
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.510 0.489 9.22 <2e-16 ***
lixo -0.396 0.195 -2.03 0.043 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 7.37 on 282 degrees of freedom
Multiple R-squared: 0.0144, Adjusted R-squared: 0.011
F-statistic: 4.13 on 1 and 282 DF, p-value: 0.043Checando os residuos para verificar a presença de autocorrelação.
Moran I test under randomisation
data: dourados.lm$lmresid
weights: pesos.viz
Moran I statistic standard deviate = 16, p-value <2e-16
alternative hypothesis: greater
sample estimates:
Moran I statistic Expectation Variance
0.520064 -0.003534 0.001130 Ajustando o modelo CAR.
Call:spatialreg::errorsarlm(formula = formula, data = data, listw = listw, na.action = na.action, Durbin = Durbin, etype = etype, method = method, quiet = quiet, zero.policy = zero.policy, interval = interval, tol.solve = tol.solve, trs = trs, control = control)
Residuals:
Min 1Q Median 3Q Max
-12.53213 -2.34032 -1.09686 0.82021 31.62992
Type: error
Coefficients: (asymptotic standard errors)
Estimate Std. Error z value Pr(>|z|)
(Intercept) 4.07199 1.54998 2.6271 0.008611
lixo -0.25129 0.14814 -1.6963 0.089826
Lambda: 0.8063, LR test value: 168, p-value: < 2.22e-16
Asymptotic standard error: 0.04158
z-value: 19.39, p-value: < 2.22e-16
Wald statistic: 376.1, p-value: < 2.22e-16
Log likelihood: -885.1 for error model
ML residual variance (sigma squared): 25.43, (sigma: 5.043)
Number of observations: 284
Number of parameters estimated: 4
AIC: 1778, (AIC for lm: 1944)Checando os residuos para verificar a presença de autocorrelação.
Moran I test under randomisation
data: dourados.car$carresid
weights: pesos.viz
Moran I statistic standard deviate = 0.78, p-value = 0.2
alternative hypothesis: greater
sample estimates:
Moran I statistic Expectation Variance
0.023005 -0.003534 0.001147 Ajustando o modelo GWR
Precisamos estimar a largura de banda “ideal” para o kernel
# Biblioteca para ajustar o modelos GWR
library(spgwr)
GWRbanda <- gwr.sel(tx ~ lixo, data=setor.sf, coords=cbind(centroides.sp$X,centroides.sp$Y) , adapt=T) Adaptive q: 0.382 CV score: 14699
Adaptive q: 0.618 CV score: 15071
Adaptive q: 0.2361 CV score: 14205
Adaptive q: 0.1459 CV score: 13337
Adaptive q: 0.09017 CV score: 12151
Adaptive q: 0.05573 CV score: 10996
Adaptive q: 0.03444 CV score: 10093
Adaptive q: 0.02129 CV score: 9759
Adaptive q: 0.01316 CV score: 9296
Adaptive q: 0.008131 CV score: 8997
Adaptive q: 0.005025 CV score: 8989
Adaptive q: 0.006388 CV score: 9000
Adaptive q: 0.003106 CV score: 9843
Adaptive q: 0.004292 CV score: 9068
Adaptive q: 0.005546 CV score: 8977
Adaptive q: 0.005868 CV score: 8981
Adaptive q: 0.005586 CV score: 8977
Adaptive q: 0.005505 CV score: 8977
Adaptive q: 0.005546 CV score: 8977 [1] 0.005546dourados.gwr = gwr(tx ~ lixo, data=setor.sf, coords=cbind(centroides.sp$X,centroides.sp$Y), adapt=GWRbanda, hatmatrix=TRUE, se.fit=TRUE)
dourados.gwrCall:
gwr(formula = tx ~ lixo, data = setor.sf, coords = cbind(centroides.sp$X,
centroides.sp$Y), adapt = GWRbanda, hatmatrix = TRUE, se.fit = TRUE)
Kernel function: gwr.Gauss
Adaptive quantile: 0.005546 (about 1 of 284 data points)
Summary of GWR coefficient estimates at data points:
Min. 1st Qu. Median 3rd Qu. Max. Global
X.Intercept. -0.3250 1.4122 3.0992 5.3977 37.5813 4.51
lixo -18.3217 -1.2222 -0.4009 -0.0615 1.5557 -0.40
Number of data points: 284
Effective number of parameters (residual: 2traceS - traceS'S): 134.4
Effective degrees of freedom (residual: 2traceS - traceS'S): 149.6
Sigma (residual: 2traceS - traceS'S): 5.447
Effective number of parameters (model: traceS): 100.5
Effective degrees of freedom (model: traceS): 183.5
Sigma (model: traceS): 4.918
Sigma (ML): 3.953
AICc (GWR p. 61, eq 2.33; p. 96, eq. 4.21): 1904
AIC (GWR p. 96, eq. 4.22): 1687
Residual sum of squares: 4438
Quasi-global R2: 0.7141 Colocando a saída do modelo dentro de um dataframe.
sum.w X.Intercept. lixo X.Intercept._se lixo_se gwr.e pred pred.se localR2 X.Intercept._se_EDF lixo_se_EDF pred.se.1 coord.x coord.y
1 4.630 6.490 -1.8955 2.412 1.718 -0.02159 2.699 2.477 0.6404 2.671 1.903 2.744 731406 7541547
2 3.935 7.884 -1.2811 2.504 1.630 1.98455 7.884 2.504 0.5043 2.774 1.806 2.774 730845 7541481
3 3.063 7.268 -1.5626 2.781 1.626 -1.85906 5.705 2.164 0.5288 3.080 1.801 2.398 730958 7541239
4 4.139 9.791 -1.1687 2.377 1.277 6.80957 8.623 1.794 0.4102 2.633 1.415 1.988 730487 7541437
5 5.541 4.586 -0.6840 2.091 1.186 -2.63011 3.902 1.525 0.6665 2.316 1.313 1.689 729874 7541446
6 6.323 3.184 -0.1699 1.908 1.104 0.02057 2.675 2.336 0.6642 2.113 1.223 2.588 729919 7541019Verificando a distribuição dos coeficientes de regressão para a variável lixo
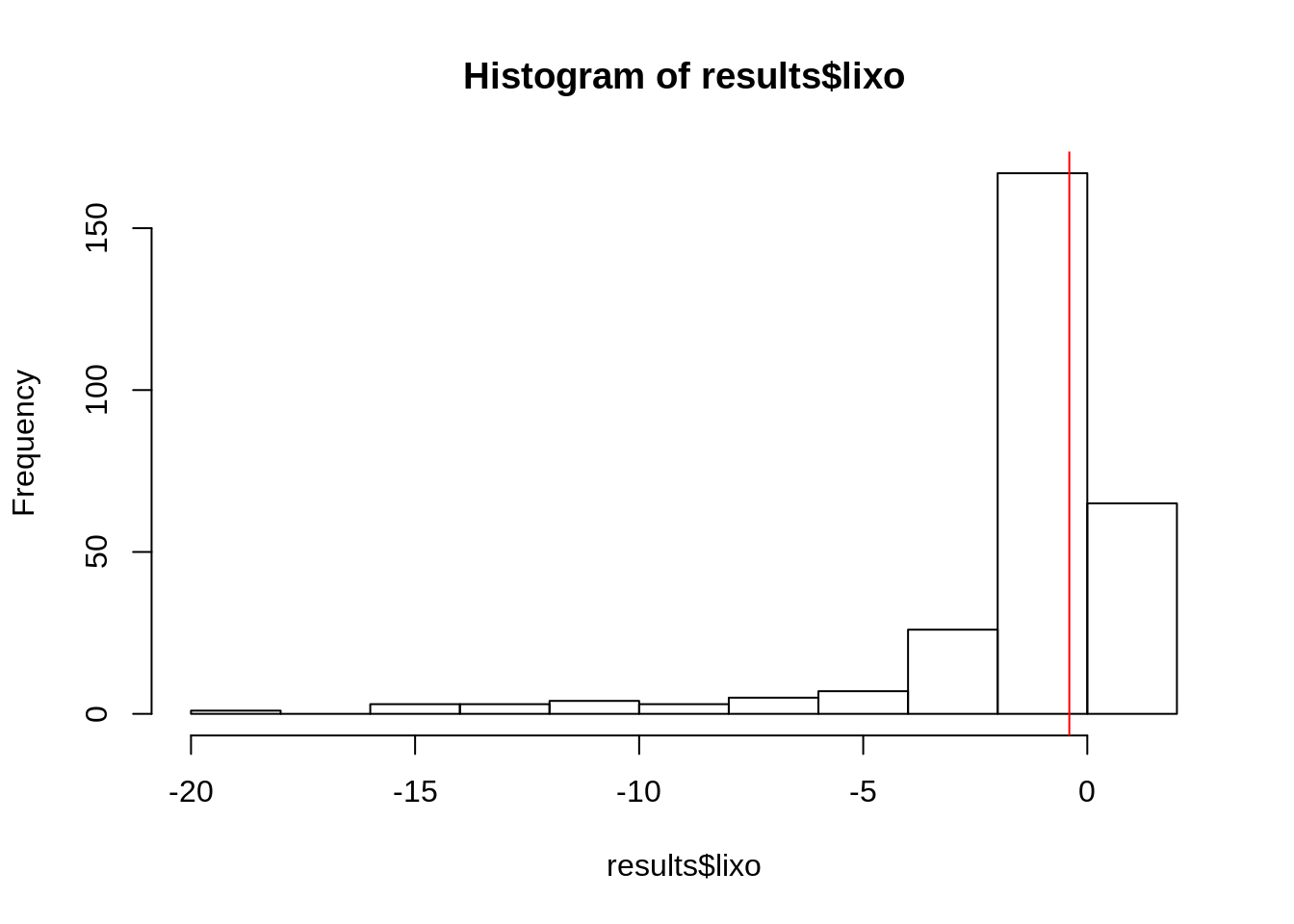
Verificando a distribuição dos localR2
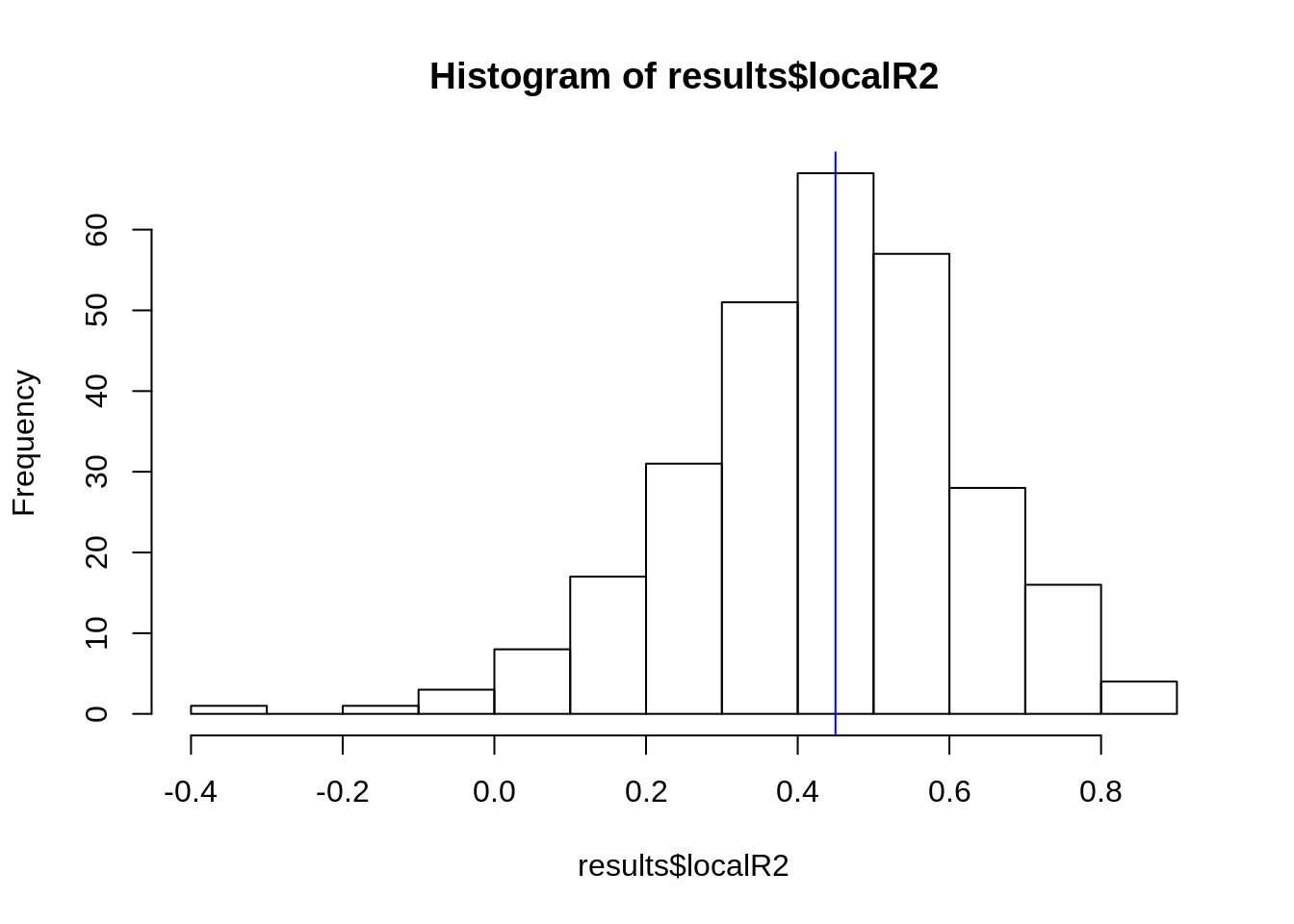
Incorporando alguns parâmetros de saída do modelo na tabela olinda.sf
Definindo as paletes de cores para a construção dos mapas.

Mapa dos coeficientes de regressão para a variável lixo
map.lixo <- ggplot(setor.sf) +
geom_sf(aes(fill = coef.lixo), color = 'black') +
scale_fill_gradientn(colours = pal) +
ggtitle("Distribuição dos coef. var. lixo") +
theme_void()
map.lixo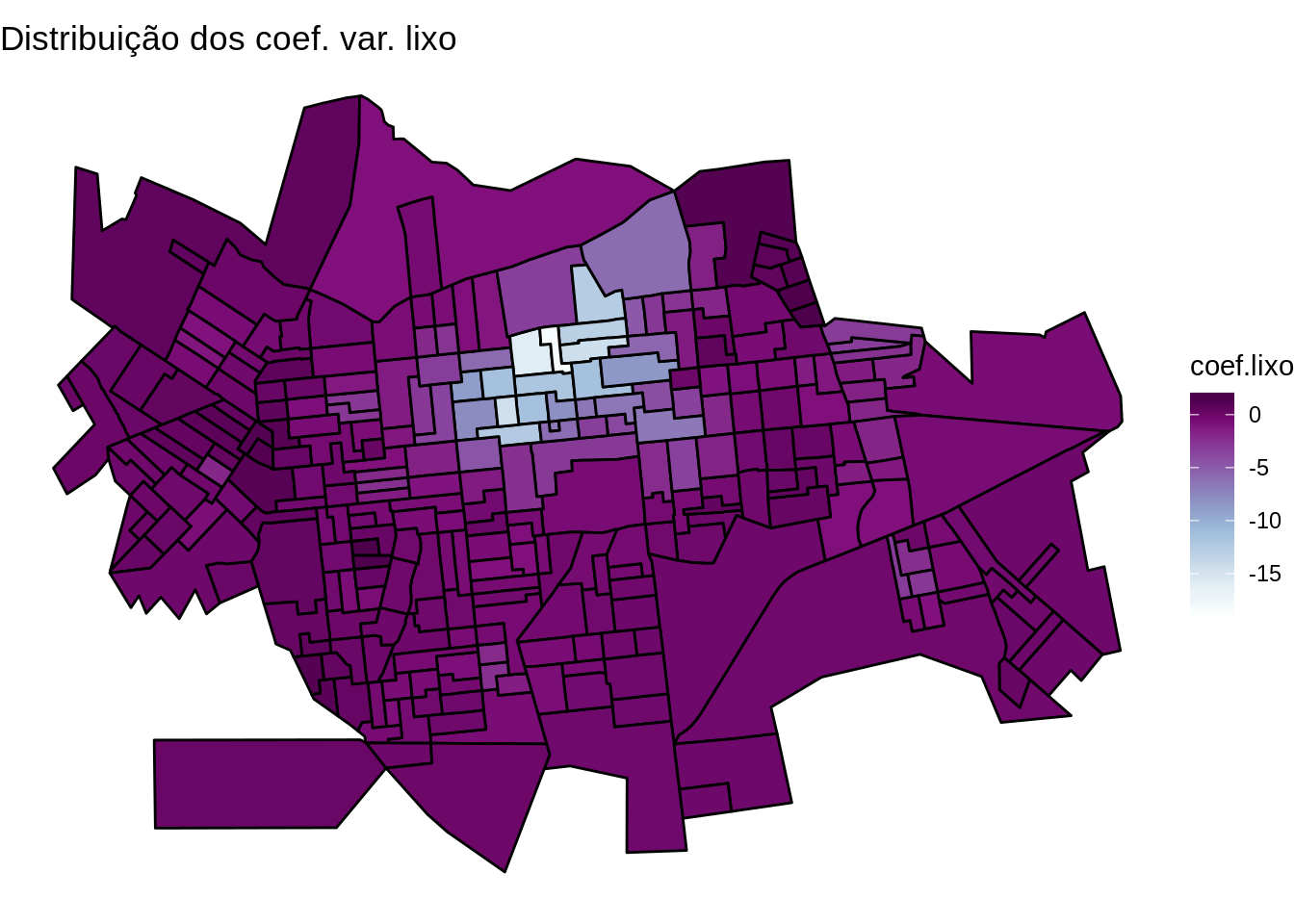
Checando os residuos para verificar a presença de autocorrelação para o modelo GWR.
# Calculando os resíduos para o modelo GWR
results$residuos <- setor.sf$tx - results$pred
moran.test(results$residuos, pesos.viz)
Moran I test under randomisation
data: results$residuos
weights: pesos.viz
Moran I statistic standard deviate = 1.5, p-value = 0.07
alternative hypothesis: greater
sample estimates:
Moran I statistic Expectation Variance
0.046817 -0.003534 0.001156 Mapeando os coeficientes de regressão para a variável lixo por significancia através do teste de wald
# Calculando a estatística de wald
setor.sf$wald.teste <- abs(results$lixo/results$lixo_se)
# Dicotomizando a estatística de wald
setor.sf$wald.teste <- ifelse(setor.sf$wald.teste < 2, 0, 1)
map.wald <- ggplot(setor.sf) +
geom_sf(aes(fill = factor(wald.teste)), color = 'black') +
scale_fill_manual(values = c("white", "purple"), labels=c("< 2", ">= 2"), name='Wald') +
ggtitle("Coef. lixo significativos") +
theme_void()
library(gridExtra)
grid.arrange(map.lixo, map.wald, ncol=2)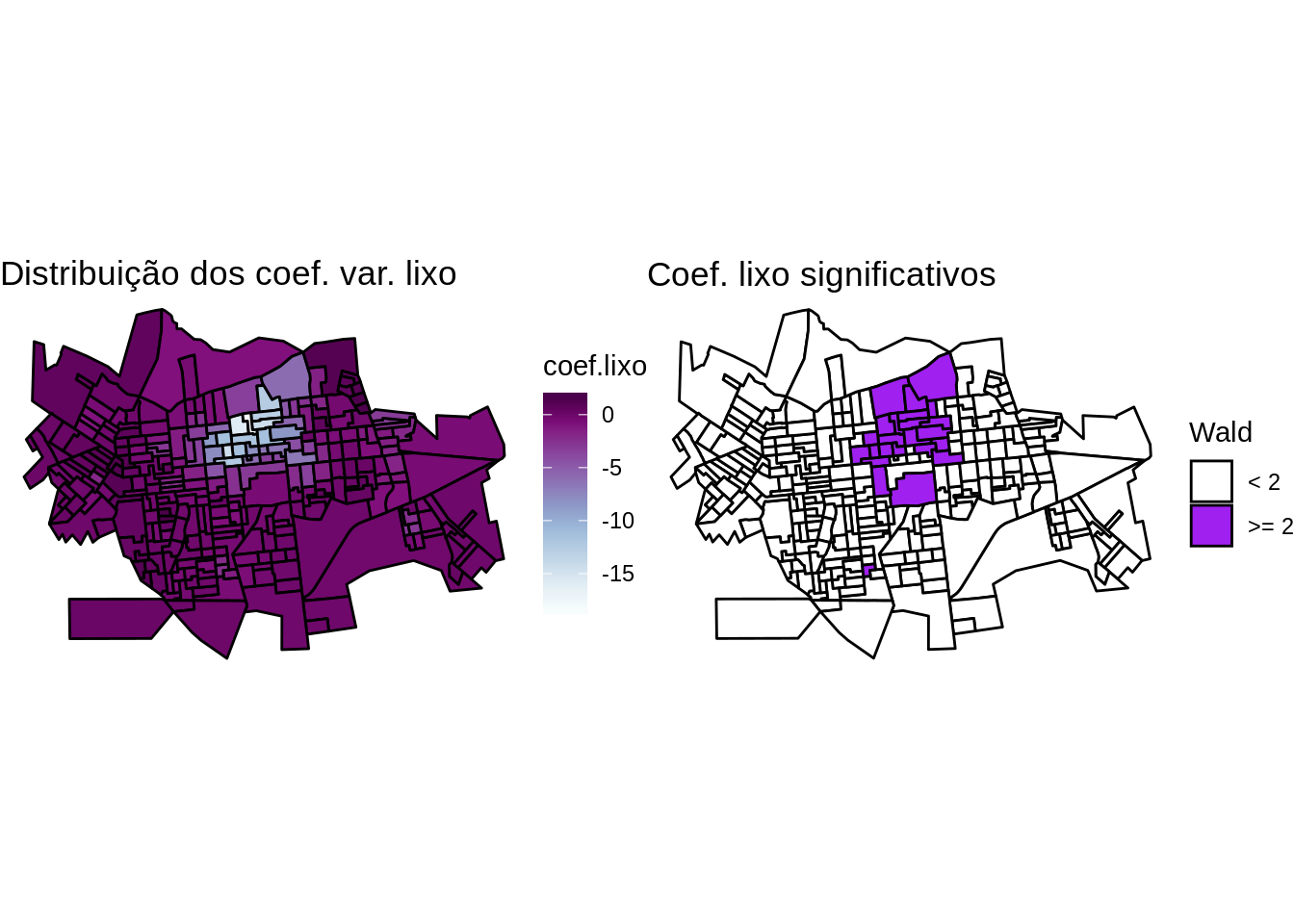
Mapa dos coeficientes de determinação regionalizados (\(R^2\) local).
ggplot(setor.sf) +
geom_sf(aes(fill = localR2), color = 'black') +
scale_fill_gradientn(colours = pal) +
ggtitle("R² local") +
theme_void()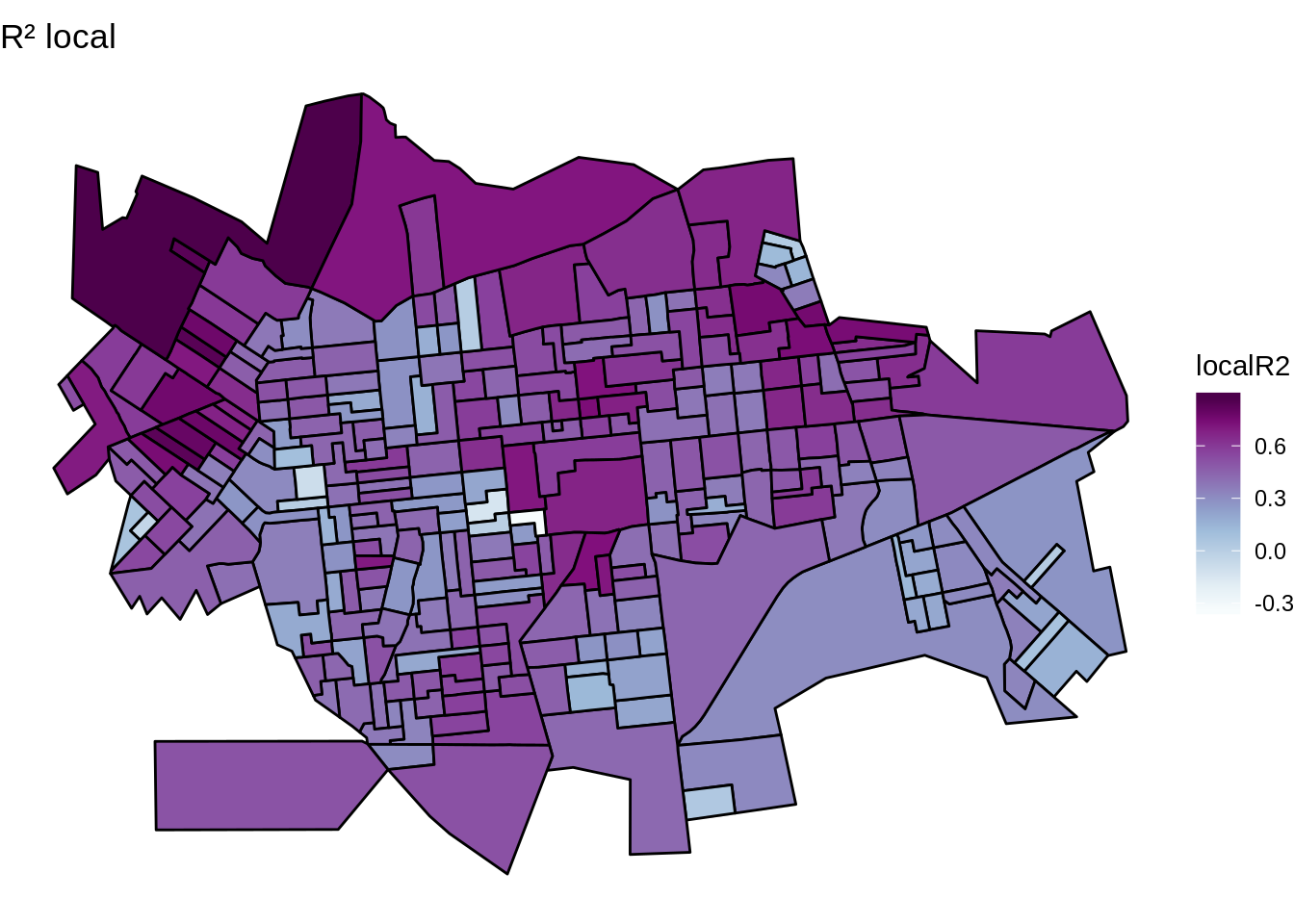
Verificando a distribuição dos preditos.
histdens <- function(x,titulo='') {
densi <- density(x)
xli <- range(densi$x)
yli <- range(densi$y)
hist(x,col="red",probability = T,xlim = xli,ylim = yli,main=titulo)
lines(densi,lwd=2)
abline(v=median(x),lwd=4,col=4,lty=2)
}
attach(mtcars)
par(mfrow=c(2,2))
hist.tx <- histdens(setor.sf$tx, "Tx Bruta")
hist.lm <- histdens(dourados.lm$fitted.values, "Pred LM")
hist.car <- histdens(dourados.car$fitted.values, "Pred CAR")
hist.gwr <- histdens(results$pred, "Pred GWR")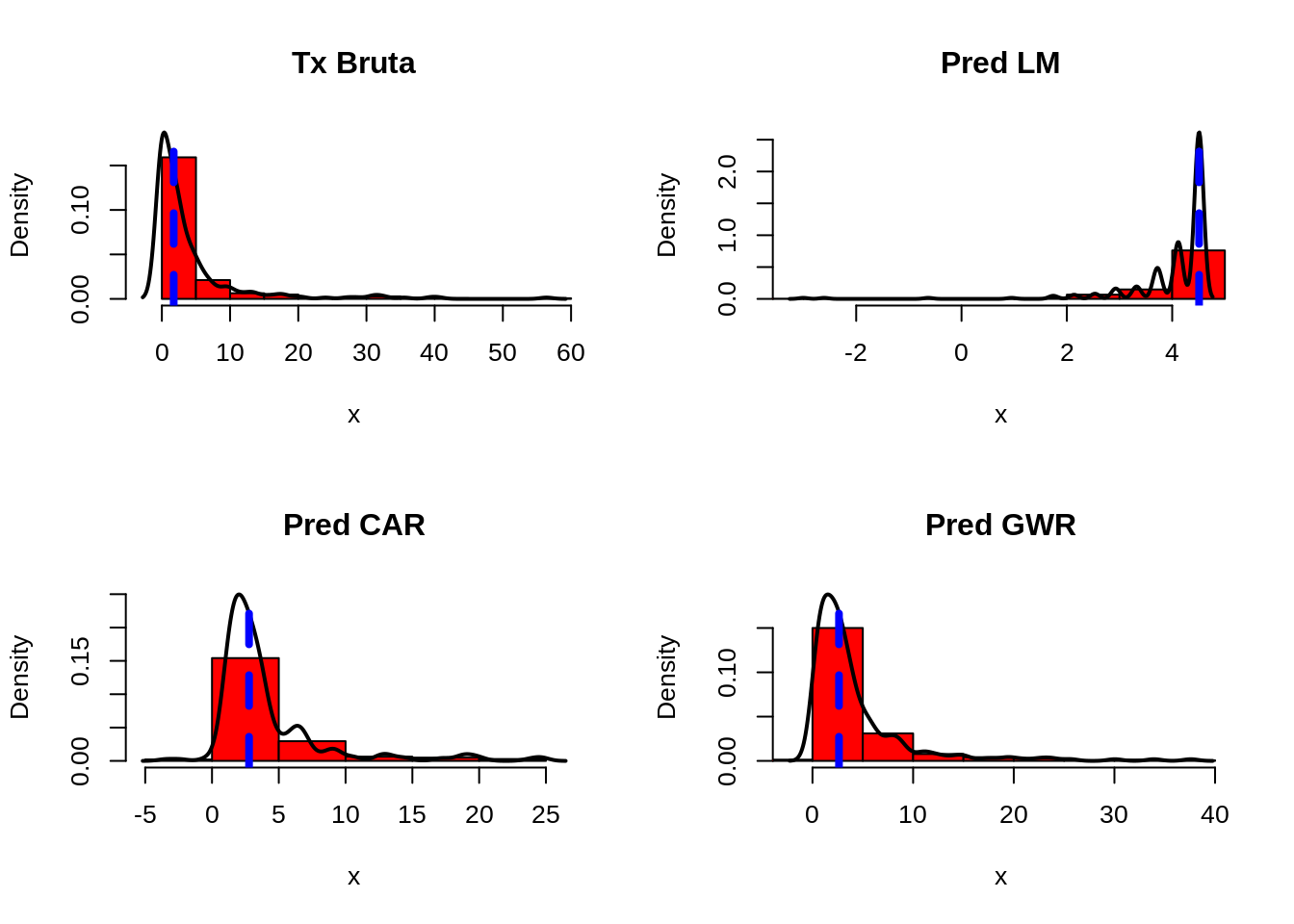
Mapeando os valores observados e preditos dos modelos ajustados
library(colorspace) #
setor.sf$brks <- cut(setor.sf$tx, include.lowest=TRUE, right=TRUE,
breaks=c(-4, 0, 2, 4, 10, 57),
labels=c("0", "0 - 2", "2 - 4", "4 - 10", "> 10"))
tx.bruta <- ggplot(setor.sf) +
geom_sf(aes(fill = brks), color = 'black') +
ggtitle("Taxa Bruta") +
scale_fill_discrete_sequential(palette ='Heat2',
c1=80,c2 =30,l1=30,l2=90,p1=0.2,p2=1.5,
na.value = "grey75",
drop=FALSE,
name='Taxa') +
theme_void()
setor.sf$brks.lm <- cut(dourados.lm$fitted.values, lowest=TRUE, right=TRUE,
breaks=c(-4, 0, 2, 4, 10, 57),
labels=c("0", "0 - 2", "2 - 4", "4 - 10", "> 10"))
pred.lm <- ggplot(setor.sf) +
geom_sf(aes(fill = brks.lm), color = 'black') +
ggtitle("Taxa Predita - LM") +
scale_fill_discrete_sequential(palette ='Heat2',
c1=80,c2 =30,l1=30,l2=90,p1=0.2,p2=1.5,
na.value = "grey75",
drop=FALSE,
name='Taxa') +
theme_void()
setor.sf$brks.car <- cut(dourados.car$fitted.values, lowest=TRUE, right=TRUE,
breaks=c(-4, 0, 2, 4, 10, 57),
labels=c("0", "0 - 2", "2 - 4", "4 - 10", "> 10"))
pred.car <- ggplot(setor.sf) +
geom_sf(aes(fill = brks.car), color = 'black') +
ggtitle("Taxa Predita - CAR") +
scale_fill_discrete_sequential(palette ='Heat2',
c1=80,c2 =30,l1=30,l2=90,p1=0.2,p2=1.5,
na.value = "grey75",
drop=FALSE,
name='Taxa') +
theme_void()
setor.sf$brks.gwr <- cut(results$pred, lowest=TRUE, right=TRUE,
breaks=c(-4, 0, 2, 4, 10, 57),
labels=c("0", "0 - 2", "2 - 4", "4 - 10", "> 10"))
pred.gwr <- ggplot(setor.sf) +
geom_sf(aes(fill = brks.car), color = 'black') +
ggtitle("Taxa Predita - GWR") +
scale_fill_discrete_sequential(palette ='Heat2',
c1=80,c2 =30,l1=30,l2=90,p1=0.2,p2=1.5,
na.value = "grey75",
drop=FALSE,
name='Taxa') +
theme_void()
library(gridExtra)
grid.arrange(tx.bruta, pred.lm, pred.car, pred.gwr, ncol=2)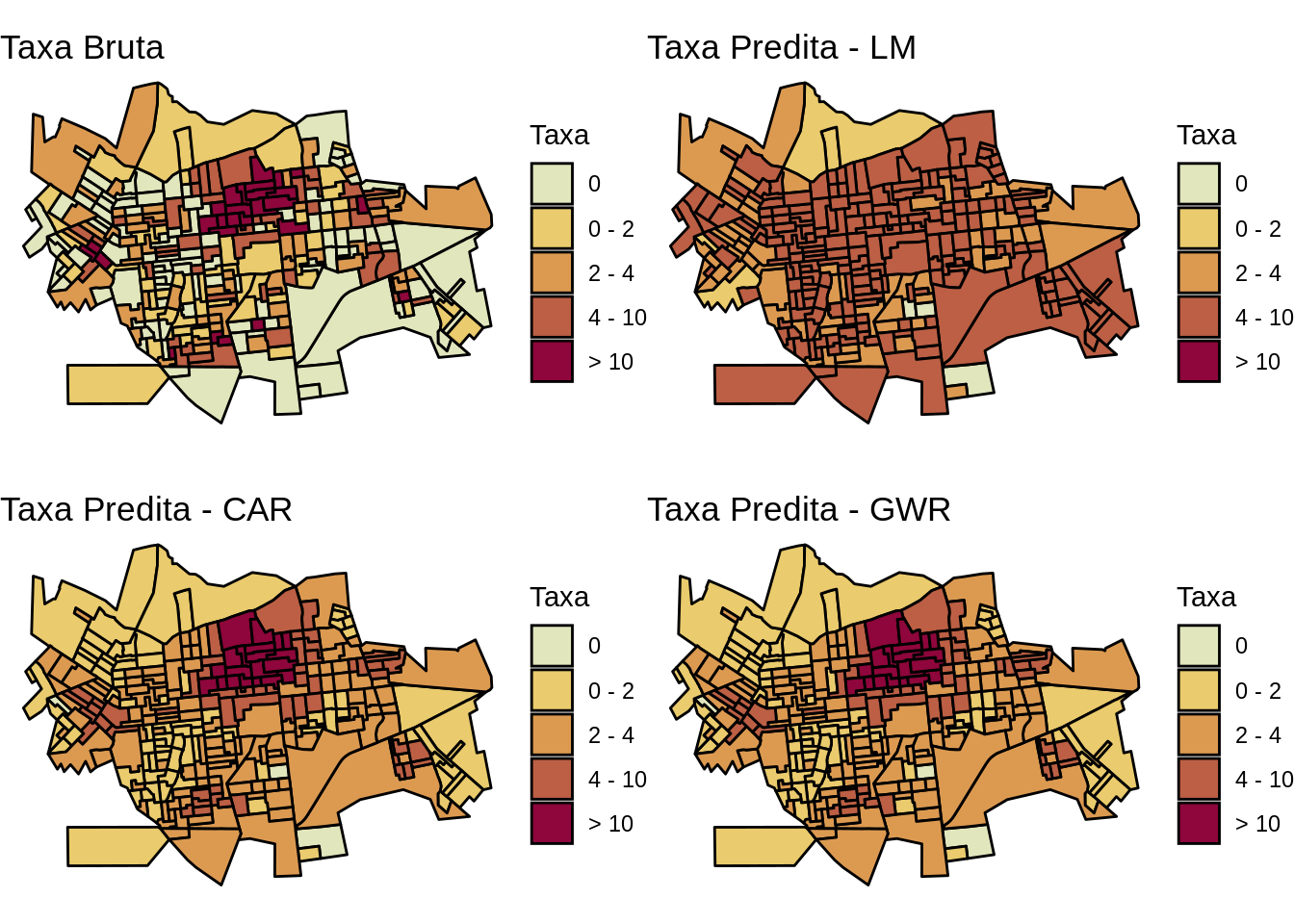
Verificando a distribuição dos resíduoas .
library(vioplot)
vioplot(dourados.lm$residuals, dourados.car$residuals, results$residuos, names=c("LM", "CAR", "GWR"), col="orange")[1] -13.14 51.89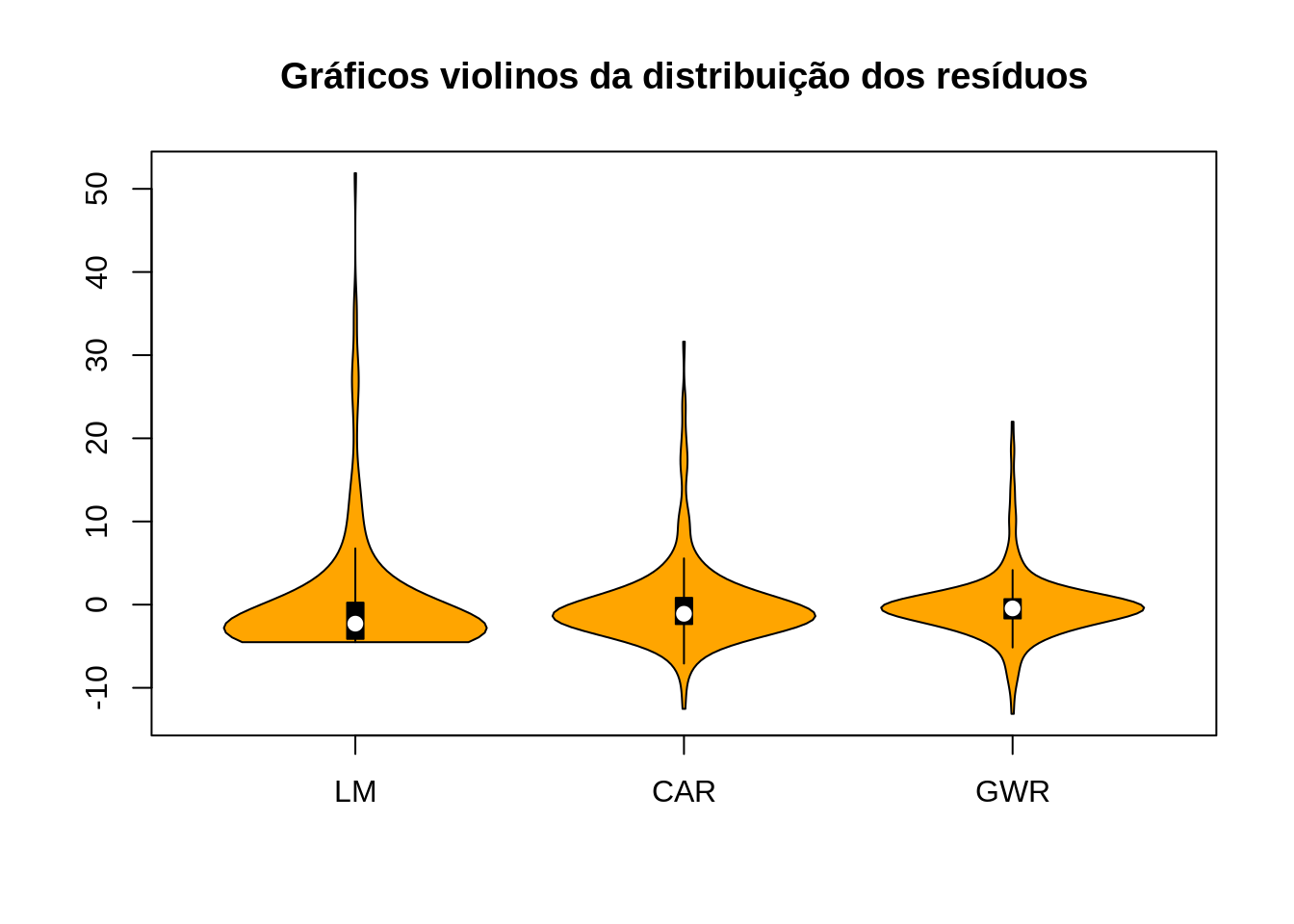
Mapeando os resíduos dos modelos ajustados
library(colorspace) #
setor.sf$brks.res.lm <- cut(dourados.lm$residuals, include.lowest=TRUE, right=TRUE,
breaks=c( -14, -5, -1, 1, 5, 52),
labels=c("< -5", "-5 a -1", "0", "1 a 5", "> 5"))
res.lm <- ggplot(setor.sf) +
geom_sf(aes(fill = brks.res.lm), color = 'black') +
ggtitle("Resíduos - LM") +
scale_fill_discrete_sequential(palette ='Purple-Yellow',
c1=80,c2 =30,l1=30,l2=90,p1=0.2,p2=1.5,
na.value = "grey75",
drop=FALSE,
name='Taxa') +
theme_void()
setor.sf$brks.res.car <- cut(dourados.car$residuals, include.lowest=TRUE, right=TRUE,
breaks=c( -14, -5, -1, 1, 5, 52),
labels=c("< -5", "-5 a -1", "0", "1 a 5", "> 5"))
res.car <- ggplot(setor.sf) +
geom_sf(aes(fill = brks.res.car), color = 'black') +
ggtitle("Resíduos - CAR") +
scale_fill_discrete_sequential(palette ='Purple-Yellow',
c1=80,c2 =30,l1=30,l2=90,p1=0.2,p2=1.5,
na.value = "grey75",
drop=FALSE,
name='Taxa') +
theme_void()
setor.sf$brks.res.gwr <- cut(results$residuos, include.lowest=TRUE, right=TRUE,
breaks=c( -14, -5, -1, 1, 5, 52),
labels=c("< -5", "-5 a -1", "0", "1 a 5", "> 5"))
res.gwr <- ggplot(setor.sf) +
geom_sf(aes(fill = brks.res.gwr), color = 'black') +
ggtitle("Resíduos - GWR") +
scale_fill_discrete_sequential(palette ='Purple-Yellow',
c1=80,c2 =30,l1=30,l2=90,p1=0.2,p2=1.5,
na.value = "grey75",
drop=FALSE,
name='Taxa') +
theme_void()
library(gridExtra)
grid.arrange(res.lm, res.car, res.gwr, ncol=2)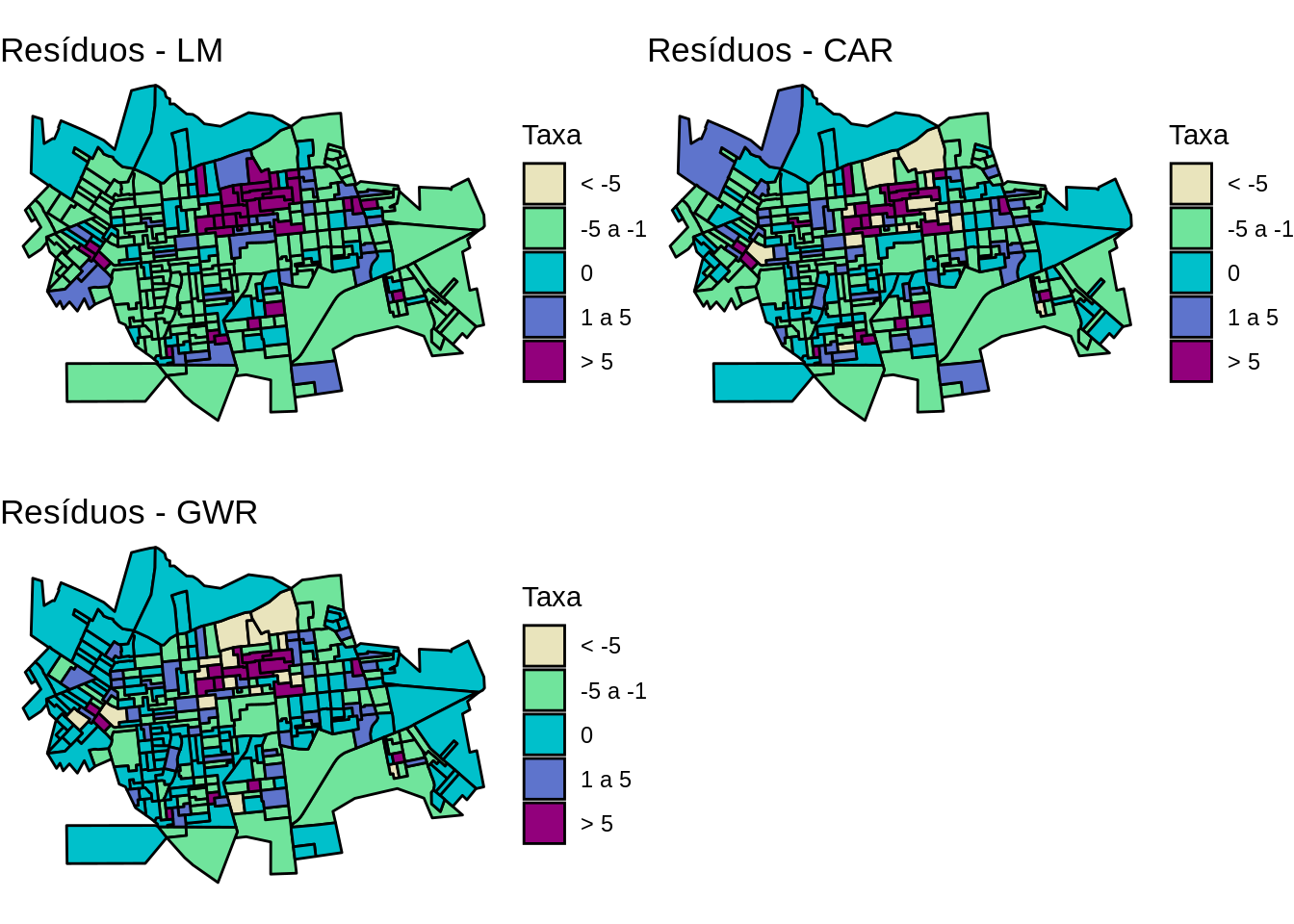
11.7 Bibliografia sugerida
Interactive Spatial Data Analysis by Trevor C. Bailey , Anthony C. Gatrell Routledge, 1995
Applied Spatial Statistics for Public Health Data; Lance A. Waller, Carol A. Gotway Wiley-Interscience 1St ed. 2004
Applied Spatial Data Analysis with R; Roger S. Bivand, Edzer Pebesma , Virgilio Gomez-Rubio Springer; Edição: 2nd ed. 2013
Online